|
|
The relatively young discipline of Generative Programming criticizes the usual OO-methodology for its primary focus on the production of a single system. It also states that creating reusable software requires a different approach. If the design is aimed towards one particular system out of a family of systems it is unlikely that the resulting implementation will be usable for other systems in that family.
Instead, software engineers who are interested in the reusability of their products should focus on a design which is targeted to a family of systems. In this paper, I will validate this new approach by designing and implementing a generic application framework for graphical editors of visual languages.
Chapter 1 gives an overview of selected GUI frameworks/toolkits, examines their design and analyzes the concepts behind them. It shows the advantages and disadvantages of those systems from the client programmer’s standpoint as well as from the system maintainer’s standpoint.
Chapter 2 analyzes various alternative design methodologies and implementation techniques. It shows how these concepts can be used to improve the flexibility and reusability of object oriented software in general and application frameworks in particular. The chapter ends with the description of WeaveJ, a tool which implements some of the ideas and concepts introduced in this chapter.
Chapter 3 describes the design and implementation of a generic, reusable and flexible application framework for graphical user interfaces which can be used to implement graphical editors of visual languages. The focus of this chapter lies on the implementation of an object-oriented constraint solver which is used to layout the components.
In this chapter I will give an overview of a choice of different application frameworks and GUI toolkits implemented in different languages. Although being far from complete, this overview should enable the reader to understand the limitations of inheritance based approaches to framework design and implementation.
The topic of this paper are frameworks for graphical editors. This chapter covers both, GUI toolkits and graphical application frameworks, because they are very similar. They are both centered around the idea of visual objects, i.e. components1. They differ in their scope and in the way they influence the application’s architecture. The scope of an application frameworks is to take care of most if not every aspect of an application. The scope of a GUI toolkit is just the components. From an architectural point of view, application frameworks are built upon toolkits. Due to their larger scope, application frameworks heavily affect the architecture of the applications.
Java is an object-oriented language with a syntax similar to that of C and restricted and stream-lined object-oriented semantics. It features robust multithreading, dynamic binding and loading; has a built-in garbage collector; and supports persistence. The platform independence of Java programs was a major objective during Java’s language design. A compiled Java program should run without modification or re-compilation on any platform for which an implementation of the Java Virtual Machine (JVM) exists.2
Java is easy to understand and is free of the obstacles found, for example, in C++. It supports distributed computing (RMI, CORBA). Java programs are relatively small, which allows code to be downloaded on demand at runtime.
Java programs are an order of magnitude slower than their C or C++ counterparts. This is true even today, although new JVM implementations (HotSpot, [SUN]) have improved performance significantly. Java has also suffered from its poorly written first release runtime library (for examples see [Bec00]) and its lack of an open language standardization process. In the past, Sun addressed both issues with the Java Community Process and improvements to the runtime library, i.e. new container classes, JFC, etc.
When Java was initially released it came with a set of packages for common programming tasks. Among them were stream and file I/O, time and date calculation, data type conversion, character string manipulation, network socket communication, object persistence and data structures (container classes). It also came with a package for graphical user interface programming: Abstract Windowing Toolkit (AWT).
According to [Eck00] the first release of AWT was designed in only one month. Because of that it seems only logical that AWT would lack many of the features which developers of real-world applications find vital. One of the most serious limitations of the first release was that the developer needed to subclass AWT components in order to handle events generated for that component. This was soon fixed for the second release, which allowed developers to add event-handlers dynamically to component instances. Unfortunately, the second release had to be compatible with the first one, which meant that both event handling schemes had to coexist. This caused some confusion among programmers.3
It was one of AWT’s major design goals that it conform to the write-once-run-anywhere strategy of its implementation language. The designers realized that there were two different ways to enforce AWT’s platform independence. The first approach made use of existing standard components native to each platform. Taking the second approach meant implementing the major part of the components in Java itself and writing very little native, i.e. platform dependent, code to access the target operating systems graphical output subsystem.
The designers chose the first approach - a component implementation in Java and native code acting as a bridge to the so called peer, a platform specific component. An example of this is a simple push button. The button component consists of a class called Button, an abstract class called ButtonPeer, and ButtonPeer-derived classes containing mainly native methods - one derivative per platform.
This approach is advantageous, in that a user of a Java AWT application is faced with the natural GUI for his/her platform. On the other hand, this approach also has disadvantages; the main one being:
Beginning with JDK 1.1, AWT allowed for ‘peer-less’ aka light-weight components, that is components without a native peer. That enabled programmers and third-party vendors to write their own pure-Java components and mix them with heavy-weight AWT components.
Sun, becoming aware of the severe shortcomings in the design and implementation of AWT, attempted a fresh start. The result was the Swing toolkit, which addresses all the above mentioned drawbacks. Swing is part of Sun’s Java Foundation Classes (JFC) and its main advantages and disadvantages are as follows:
Since I will repeatedly refer to the Observer pattern, it would be helpful to understand why this particular pattern is so important for GUI programming. Usually a user interface is a graphical representation of a programs internal data. The representation used may be for viewing only or it may allow the user to manipulate it and thereby manipulate the represented data. It is essential to establish a synchronization scheme between the representation and the data such that both remain consistent. Additionally, there may be different possible representations of the same internal data. In some cases multiple such representations need to be visible simultaneously.
All the above mentioned features recur in almost every program that has a graphical user interface. From recurring features and program behaviour a Design Pattern[GHJV95] can be extrapolated. The design pattern I describe here is commonly known as Observer.5
In Swing almost every component acts as a listener (Observer, in the standard pattern). To use this component, the client has to implement the corresponding model interface. The model declares methods that will be invoked by the component after the model has informed the component about changes in the data.
The JList component, for example, implements the ListDataListener. This interface contains methods which notify the list about certain changes in the underlying data. There is also the ListModel interface, which must be implemented by the client. This interface contains methods for registering and unregistering a listener (Attach() and Detach(), in the standard pattern), retrieving an element by its index and getting the total number of elements to be displayed.
Each component makes certain assumptions as to how the data it displays is structured. A text field requires a character string, a list requires a one-dimensional field of elements and a table requires a two-dimensional field of elements. It is therefore necessary that each component defines its own pair of model and listener.
The registration of listeners and their notification is something all models have to do. This suggests that application specific models should inherit from some toolkit/framework-specific parent class which implements the shared behaviour. Unfortunately, models in Swing are interfaces and as such cannot contain or inherit functionality. Therefore, Swing provides abstract helper classes, which are incomplete implementations of the model interface and which relieve the application programmer from the burden of managing the listeners. The application programmer can use the helper as the base for his/her own implementation of the model.
This approach becomes problematic when one application class wants to serve as a model for multiple different components. Dialog windows are examples of such classes. Swing application creates a dialog window by deriving Swings’s JDialog class. The components on the dialog are created during the initialization of the dialog subclass. If the dialog contains a list and a tree component, the dialog subclass would have to implement two different model interfaces: ListModel and TreeModel. The helper classes would be useless in this case, because helpers need to be extended and the application specific dialog class already extends JDialog.
Multiple inheritance would resolve the problem but Java does not have multiple inheritance. Instead, Java has inner classes. The dialog subclass of the above example can use non-static inner classes for each model. The inner model classes can extend a helper class and have access to their outer class’ members.
__________________________________________________________________________
Inner classes in Java are classes whose definition is nested inside another class
definition. There are static inner classes whose purpose is mainly better code
organization, i.e. keeping related things together and preventing name space
pollution.6
Non-static inner classes additionally have access to all of their outer class members. To do so, every instance of a non-static inner class keeps a hidden reference to the outer class instance that created it. Furthermore, an inner class (static and non-static) can extend any class or implement any interface, completely independent of its outer class. Java’s non-static inner classes are an example of using object composition as an alternative to multiple inheritance. Instead of having the outer class C extend more than one base class (B0, B1, B2, ...Bn) one could have C create instances of inner classes Ii each of which extends one of the base classes Bi except B0 which is extended by C. Instead of handing out a reference to itself when a Bi sub-type is required, it hands out the reference to an instance of Ii.
Thus, the inner class objects have access to the outer class object and more than one
base-class can be extended. The major disadvantage of this technique (and others using
object composition) is object schizophrenia which will be examined in later
sections.
__________________________________________________________________________
In the world of object oriented programming, inheritance plays a major role and has often been claimed to be the main concept behind reusable software. Unfortunately, this claim has not been lived up to. In this section I will analyze why. According to [Boo94], software reuse can be achieved in different ways:
“Ultimately, software reuse can take on many forms: we can reuse individual lines of code, specific classes, or logically related societies of classes. Reusing individual lines of code is the simplest form of reuse. . . . We can do far better when using object oriented programming languages by taking existing classes and specializing or augmenting them through inheritance. We can achieve even greater leverage by reusing whole groups of classes organized into a framework.”
The first observation is that code reuse can be accomplished at different levels of granularity. Another observation is that the intent of reuse increases with the level of abstraction. A person writing a single line of code or a even a whole method does not intend for someone to copy it into a different project later on. It is much more likely that a person which designs a class, does so with the intention to enable someone else to reuse the class by inheriting from it. Finally, a framework is certainly designed to be reused. In this thesis I will focus on the reuse of single classes and the reuse of frameworks. Inheritance is probably the most widely used way of reuse on a per class level. This is why will start with an analysis of reuse through inheritance. The reuse of whole application frameworks follows in sections 1.3, 1.4 and 1.5.
Probably the most common pitfall for programmers regarding inheritance is the lack of distinction between all the different effects it has on the inheriting class as well as the inherited one:
The problem with class inheritance is that if you need one effect you will automatically get the others as well.8 The following example will illustrate this.
Imagine that you are an application developer in a small software consulting firm and you are assigned to a project for a larger company. Your part of the project is the front-end, which will be employed by its users everyday to enter large amounts of data. The front-end will comprise a dozen different forms, each containing 10 to 30 components - mostly text fields, push buttons and lists. Due to the amount of data, the users request that they be able to operate the whole front-end using keyboard keys only. For certain reasons the program is written in Java and since the GUI builder used in your company only supports AWT, you are forced to use AWT.
Unfortunately AWT does not fully support keyboard navigation in an intuitive manner. AWT adheres to standard GUI guidelines for keyboard input and therefore the navigation between fields is done using the tabulator key. The return key closes the form as if the OK button had been clicked. The users however, request be able to navigate between fields using the arrow keys and that hitting the return key advances to the next field. Because of this and other requirements you decide that you need to add some functionality to every AWT component class that you use.
Adding functionality to classes for which you do not have the source is generally done using inheritance: you inherit from the class to be extended and add the necessary functionality to the derived class. This approach becomes problematic when you need to add the same functionality to several classes. Provided that all inherit from a common base, one might be tempted to derive from their base. In your case the common base is java.awt.Component, the super-class of all the components on your forms. You can, of course, derive from java.awt.Component but you would also need to make the component sub-classes (lists, buttons and text-fields) inherit your new common base (figure 1.1). With Java this is not possible without modifying source code, which may not be an option because you simply do not have the sources or because you are not willing to re-apply the changes to every new release of AWT. Generally, it is virtually impossible to insert a Java class into the inheritance lattice.
|
|
Theoretically, making a Java class inherit a different super-class is possible by modifications on the byte-code level. The binding between a class and its super-class is rather weak (just a few entries in the class file’s constant pool). If the new super-class is a derivative of the old super-class the modifications should be transparent to all sub-classes and the old-super class. A language which supports dynamic inheritance (SELF) will be introduced in section 1.6.
The only option left is to derive from every component class which you use, namely Button, Textfield and Choice. The functionality that you initially wanted to be shared is going to be duplicated in all three derived classes.9 To lessen the impact of duplication, you decide to encapsulate that functionality in a separate class and to forward requests to an aggregated instance of this class from within the derived component classes.10
For other reasons you also have to add a minor feature to the text field class.
(This example is based on a real world project and the true reason for the tweak
is rather complicated. In fact, it is a work-around for a bug introduced by a third
party extension to text fields). The text field class has a method called select()
which marks the whole text in the text field component. What you need to do, is
to fake the return value of the getText() method while select() is
active.
private int inSelect = 0;
public String getText( ) {
// when select() asks for the text
if( inSelect > 0 ) {
return String.rtrim( getFormattedText( ) );
}
}
public synchronized void select( ) {
inSelect++;
// we know that super.select() will call getText()
super.select( );
inSelect--;
}
This work-around is only possible because of the tight coupling between
super-class and sub-class. There is nothing bad about this particular work-around,
other than that it may only work for the current release of AWT. For a
work-around this is acceptable. What is harmful, is that those kinds of
dependencies between derived and deriving class are possible and even encouraged
by inheritance-based object oriented languages.
The intimate knowledge which a deriving class has about its super class breaks encapsulation and violates the hiding principle of software engineering. This is why inheritance is referred to as white-box reuse as opposed to black-box reuse [Szy99]. This hiding principle, separating interface from implementation, is a primary prerequisite for the creation and maintenance of reusable class libraries. Inheritance is often regarded as a way of reusing and customizing the classes in the library. In reality it makes the maintenance of libraries harder because it increases the likelihood that a change to a library class - while still in accordance with the interface contract of that class - breaks classes derived from the changed class. This problem is also referred to as the Fragile Base-Class Problem [Szy99]: modifying the base class might (1) break classes derived from it or (2) make it necessary to recompile the derived classes. In Java the second case can only be caused by modifications to the interface of a class.11
Most OO-languages offer the option to restrict the access from sub-class to super-class. For example, in Java one would use the member access modifier private to prevent sub-classes from accessing a particular super-class member (method or field). Nevertheless, it is still possible for the sub-class to override any non-private method in the super-class. This introduces the above mentioned dangerous dependencies between sub-class and super-class. Java has a keyword to control the overriding of class members (final). Conscious use of this feature can definitely be used to tame inheritance based reuse. Unfortunately, that would also limit the flexibility of the framework user. Overriding is one of the key aspects of inheritance and restricting overriding questions the whole concept of inheritance. It would be much better to switch to a different language idiom to achieve reuse. These alternatives will be examined in the next chapter.
The following list summarizes the drawbacks of inheritance.
These are very general statements and wherever there is a rule there also is an exception. There are languages that support dynamic inheritance (SELF). Other languages support parameterized inheritance (C++ templates) and still others have a dedicated concepts for interfaces and inner-classes (Java). This just shows that language designers have searched for alternatives. Some of the techniques and tools which will be examined shortly are based on these alternatives.
Unidraw [VL90] is a framework for building graphical editors written in C++. One of its authors later participated in the research on design patterns, some which can already be found in Unidraw. In this section I will analyze how multiple patterns were incorporated into the same design and address selected design decisions made by the authors of Unidraw.
A design pattern is a way of reusing pieces of software design as opposed to reusing pieces of the software itself. It is a way for experienced software developers to share their knowledge. Although a pattern is something that appears in recurring instances, the applications of a design pattern do not necessarily look identical. A design pattern is usually discovered by analyzing and extracting the similarities between solutions to recurring problems. Design patterns also aid in documenting and understanding software because they establish common terminology and because they structure the design into recognizable pieces. Design patterns focus on the collaboration between objects, whereas traditional object oriented design often focuses on the features of objects and their classification into a hierarchy of generalizations, i.e. classes.
Design patterns are extracts of designs. For the creation of real-world applications and frameworks the reversed process of pattern discovery has to be used; that is, patterns which existed separately before have to be combined with each other - the patterns have to be woven.
Many patterns consist of collaborating objects. Because objects in most OO languages are instances of classes we can also say that classes define the collaboration. Each class taking part in a collaboration is assigned to a role. If software uses more than one design pattern, it is likely that one class plays more than one role simultaneously. So, the process of pattern weaving involves incorporating more than one role into a class. This can be done in a variety of ways. I will examine the different techniques in the next chapters. For now I will focus on an analysis of how Unidraw combines patterns.
The two most central patterns in Unidraw are Observer and Composite.12 The Composite pattern is used to compose objects into a tree structure representing part-whole hierarchies. It lets clients treat individual objects and compositions uniformly. In the Composite pattern the interface of compound objects (objects made of other objects) is the same as that of atomic objects.
Treating composite and atomic object the same may be advantageous for the traversal of the object tree but it leads to the anomaly that atomic objects have a method to add another object to them. Calling this method will cause an runtime error. The Composite pattern trades type safety for transparency (uniform interfaces of atomic and compound objects). There are alternative implementations which are especially useful in languages which offer run-time type checking, e.g. Java.
In Unidraw the two patterns are combined as follows: the roles of the Observer pattern (subject and observer) manifest in two classes - Component and ComponentView. Each component is a pair of Component and ComponentView instances. In addition to the methods needed for the roles in the Observer pattern, both classes also contain methods for iterating over the children. The default implementation of these methods is empty in both classes. For atomic graphical components (components that are represented by visible objects and do not consist of other objects) there are the GraphicComp and GraphicView classes. Compound graphical components are implemented by the classes GraphicComps and GraphicViews. A UML class diagram of this can be found in figure 1.2.
In Unidraw the interface to compound and atomic components is not as uniform as the standard Composite pattern suggests. It is split into two pieces, child traversal and child manipulation. The traversal interface is indeed uniform - even atomic components have it. The manipulation interface is introduced by compound specializations of Component and ComponentView, e.g. GraphicComps and GraphicViews. This has the advantage that the manipulation interface can be constrained to a particular type of children.
A disadvantage of this technique is the need for duplication of child manipulation code. Of course, there are remedies for this problem (delegation, forwarding) but it still obscures the design. In section 2.4 I will show how type safety can be achieved while avoiding duplication.
One also observes what appears to be a minor anomaly in the Observer pattern. Graphical objects like points, lines, rectangles or text, which one would intuitively characterize as pure views, are modeled in Unidraw as components, thus consisting of a subject (GraphicComp) and a view (GraphicView). This leads to the interesting perception that there seems to be a symmetry between subject and view: each view is also a potential subject of another view, which in turn might be the subject of another view, and so on. In [VL90] the authors of Unidraw differentiate “between (1) the state and operations that characterize objects and (2) the way the objects are represented in a particular context.” Apparently, an object’s representation is the state of another object, and this state can be subject of another representation. Unidraw does not offer this flexibility - an object can either be a subject or a view, but not both.
In some cases it can be useful to be aware of the subject-view symmetry. For example, the UML standard defines models as complete abstractions of systems, and diagrams as graphical projections of (subsets of) models [SA98]. This is very close to the idea of the observer pattern. A hypothetical UML authoring tool would use the observer pattern internally to represent the interdependencies between the logical model, e.g. the classes, their members and their relations, and the graphical projections of the model, e.g. class diagrams. Interestingly, the UML standard does not only employ diagrams and models. It also defines a meta-model13 which is needed to specify the UML standard using a subset of UML itself. It is organized into different diagrams, each describing a the system from a different perspective. The perspectives are (source: [SA98]):
It would make sense to mirror UML’s meta-model concept in the architecture of an hypothetical UML authoring tool, such that the meta-model is the abstraction of the system to be modeled. It describes the system on a very general level. This meta-model would be observed by models -- one for each perspective -- which in turn would be observed by the corresponding diagrams. Consequently, a model is both, subject and view, and it plays both roles simultaneously.
Therefore, any modern GUI application framework should support the subject-view symmetry as an integral part of its design. The easiest way to do that is to put subject and view functionality in the base class of the class hierarchy. For example, the ET++ framework which will be described briefly in section 1.5 does that in its VObject class -- the base of all other visual object classes. But doing so leads to overweight base-classes and blurs the conceptual distinction (separation of concerns) between a subject and a view. Ideally, subject and view functionality should be defined and implemented in separate units (classes or interfaces) but there should also be a mechanism to merge the subject and view functionalities in case an application has classes which play both roles simultaneously.
So far I have discussed how Unidraw employs consistency of representations and part-whole hierarchies. Both are important concepts in the domain of graphical editors. Another concept is layout.
The term layout describes the physical arrangement of components on the output device, affecting their size, position and Z-order.14 The simplest way to layout a toolkit’s components is to have the application programmer manually define the fixed position and size of components. Using a GUI builder in which the programmer can drag components or specify primitive layout rules (grid, position and size alignment) is definitely more satisfying and productive. Sometimes an application allows the user to change the size of the forms. An adjustment of forms to different screen sizes may also be desirable. Resizing a form requires a run-time revalidation of the layout, which is not possible if the coordinates are fixed. For this purpose, most toolkits provide special layout classes that allow a higher level means of arrangement of components. Some GUI builders also support interactive composition and manipulation of such abstract layouts.
A toolkit’s layout classes often assume that the components have rectangular bounds. Although this might be appropriate for GUI toolkits, such a simplification is not reasonable for graphical editors. Consequently, Unidraw provides a much more sophisticated layout.
In Unidraw there are special graphical components called connectors. The connector’s subject is used as a child of subjects belonging to compound graphical components. There is a view for connectors too (a crossed circle), but most compound graphical components omit it in their own view. A connector can be one of three types: pin (zero degrees of freedom), slot (one degree of freedom), and pad (two degrees of freedom). When combined in pairs, connectors form a connection. When a pin is connected to another pin, both will always have the same coordinates. A pin connected to a slot can move along the slot but must stay within the slot’s bounds. A pin connected to a pad can move in both dimensions inside the pad’s bounds. Figure 1.3 illustrates examples of connectors.
Connectors also have a mobility attribute, which can be fixed or floating. This attribute determines which of the connectors in a connection actually moves to satisfy the connection’s constraints. Furthermore, each connection is associated with a piece of “glue” which determines its elasticity and deformation limits.
The layout model is solved by a rather monolithic CSolver class, which solves a network of connections by recursively reducing the connection network. The reduction take place when the solver finds a primitive combination of connections like parallel and series connections. The solver temporarily replaces the combined connections with a single equivalent connection and carries on with the reduction until all connectors are fixed or when there is just one connection left. On return from each level of recursion, the solver reconstructs the original network by applying the deformation of the equivalent connection to each of the original connections.
Unidraw’s layout model is a very mechanical one, making it predictable and logical for both the user and the programmer. The downside of mechanical models is that they might take a longer time to solve than simpler models. What all these layout models have in common is that they describe a set of constraints and that these constraints are solved in order to compute the actual geometry of the components. The type of constraints which describe a layout of graphical components needs to be simple enough such that they can be solved within fractions of seconds. This is because the user should be able to modify the layout interactively. On the other hand, the more powerful constraints are, the easier it becomes for the programmer to describe the layout. Therefore, the designer of an GUI application framework has to find a good tradeoff between the constraint’s complexity and the responsiveness of their solution algorithm.
Some graphical editors may need a layout model with a simple constraint requiring that the components do not overlap. The user can freely drag components around, and the dragged components could “push” the other components aside, just like coins on a table. The constraints in this layout model form a system of linear inequations. Assuming that all components have rectangular bounds and each component has a top, a left, a bottom and a right edge, there would be one equation for every pair of components. For example, two components c1 and c2, each having four edges t1, l1, b1, r1, t2, l2, b2 and r2, yield the following inequality:
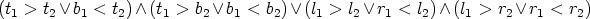
For n components n2 inequalities of the above kind are needed.
This type of constraint cannot be modelled using Unidraw’s connectors. This is because UniDraw does not support the disjunction of constraints. It is impossible to specify that a component may either appear to the left or to the right of another component. In most cases this is not even necessary and Unidraw’s model is sufficient. Ideally, an application framework for graphical editors should employ a means of exchanging the layout model. Based on the simple assumption that components have rectangular bounds, many different types of constraints are possible -- for example, the mechanical Unidraw-like type or the above inequation type.
Sometimes it is useful to send arbitrary messages to objects without having to (1) declare reception ability, i.e. to ensure that the message is implemented in the receiver and (2) know the receiver in order to issue the message. It is not possible to implement messages like that in C++ or Java using plain methods because method invocation always presumes a receiver instance.
The need to declare the reception ability can be avoided when using virtual methods: The base class of all receivers defines one virtual method for every type of message to be received. In the base-class this method has an empty body. If a receiver wants to implement a particular message it simply overrides the corresponding method. Thus, every message can be sent to any receiver, regardless whether the receiver implements the message or not. If the receiver does not implement the message, it will be caught by the base-class. The downside of this approach is that the base-class needs to be modified when new types of messages are added to the system.
Unidraw uses a variation of the Command design pattern for this purpose. The command pattern “lifts” messages from ordinary methods to objects and makes them first-class citizens. One advantage of the command pattern is that the receiver of a message does not have to be specified when the message is sent. Instead, a reference to the receiver is stored within the command object and the reference is set when the command is created. Usually, the receiver creates the command object and registers it with the sender. The command pattern decouples sender and receiver because the sender does not need to know the receiver of a message.
Another benefit of this pattern is that only one receiving method needs to be declared in the base-class for the receivers. When new types of messages are added to the system, the receiver base-class does not need to be modified. As a result the base class stays lean and manageable. The downside of this is that the messages type has to be decoded in the receiver. If a receiver implements many different messages, this will lead to large switch statements or long chains of if statements.
Furthermore, commands can be used to parameterize the sender. Parameterization in this context means that the sender can issue a command without having to know the particular type of command it issues.
InterViews [LCI+92] is a sophisticated class framework featuring everything from simple geometrical shapes and text up to interactive components (widgets). In InterViews even primitive geometrical shapes and text characters are modeled as objects and the widgets are made up of those primitives.
This is very different to Java’s AWT and Swing where, mostly due to performance reasons, the components simply invoke methods that draw points, lines, boxes and text. AWT/Swing’s and InterViews’ approach differ in the level of physical (object-structural) granularity. In AWT and Swing the most granular object is the widget (aka. component in Java terminology) whereas InterViews’ most granular object is a glyph. In InterViews all visible objects, e.g. points, lines, characters, character strings and even whole popup menus are glyphs. Furthermore, AWT and Swing are not only of limited granularity, they also do not allow true composition of objects - the most central aspect of black-box software reuse. In AWT there is the special component Container which is a direct subclass of Component. But as its name implies it does nothing but contain other components and perform the related activity like input focus handling and layout. The relationship between object composition and black-box reuse will be subject of section 1.6.2.
The problem with the AWT approach is again the amount of duplicated functionality. Soon after AWT was released, third party vendors offered additional components or even sets of components that would replace the original AWT components. If you look at KL-Groups’ tree and table components [KLG], you will find that they completely draw themselves using the drawing primitives in java.awt.Graphics. There is no sign of reuse. In Swing this situation has improved. JTable, for example, uses a variable component to render the cell values. This cell-renderer is implemented in a similar way to a Flyweight, (see section 1.4.1) in a rather awkward way.15 The problem of limited granularity persists in Swing.
The downside of fine-granular component structure is the sheer amount of objects and the resultant quantity of storage. The Flyweight pattern deals with this problem and the authors of InterViews were some of the first to discover it. The Flyweight allows sharing of objects by making the important distinction between intrinsic (context-independent) and extrinsic (context-dependend) state. Conceptually different objects, meaning objects that have different extrinsic states but an identical intrinsic state, share one class instance. To perform an operation, i.e. invoke a method on the shared instance, the client has to pass the extrinsic state as an argument to the operation. For a more detailed description see [GHJV95].
The Flyweight in InterViews is the glyph object. The Glyph class does not incorporate any state at all. Sub-classes of Glyph may decide to share instances by making the above mentioned distinction between extrinsic and intrinsic state. Sharing of glyphs creates a glyph structure that is no more purely hierarchical; instead it forms a directed and acyclic graph.
Although a glyph is defined in InterViews as “visual data” it can also be invisible. Often invisible glyphs are used to decorate visible ones. The term decoration originates from the Decorator pattern. A decorator adds responsibilities to the object it decorates and its interface is usually wider than that of the decorated object. The base class for decorating glyphs in InterViews is Glyph’s sub-class MonoGlyph, which simply adds a method for setting and getting the body, that is, the decorated glyph. A typical mono-glyph is InputHandler which can be used to add event-handling to glyphs.
Every glyph may contain other glyphs, but there is also the special class PolyGlyph, which adds detection of structural changes. Apparently, the interface of composite glyphs is spread over two classes: Glyph and PolyGlyph. The same approach can be found in the Composite pattern, allowing for uniform treatment of atomic and compound glyphs when traversing the glyph structure.
Components often have properties like color and font that determine their appearance. Most GUI toolkits implement such properties as attributes of their component classes. In this case, every component has methods for setting and getting its property attributes, e.g. foreground or background color. Text components also have methods for setting and getting text-specific attributes, e.g. justification or font name.
However, most applications use uniform colors and fonts for all components on their forms. Not doing so would make the user interface look distracting, to say the least. Therefore, all components usually have the same set of properties. Thus, the property attributes in most components have the same value which wastes space for object storage. Furthermore, code needs to be written to set the properties of every single component in the application unless the default values of the properties are used.
InterViews uses styles to decouple the component’s properties from the components. Glyphs which have the same set of properties all share one style. A style is a set of pairs <name,value>. Both, name and value are strings and as such lack type-information.
As the idea of letting components share sets of properties is very innovative, its implementation in InterViews leaves room for improvements. For example, property values should not be strings in order to enforce some degree of type-safety and to eliminate the conversion from strings to actual values. For example, RGB color values should be stored as instances of a Color class or triples of integers rather than strings like "12,34,56". Also, there is no need to identify properties using strings. Integer keys allow for faster lookup and need less storage.
Toolkits with fine granular component structure often need to assist clients in object composition and creation. InterViews has several classes which specialize on the production and assembly of components. This concept also manifests in two design patterns: Abstract Factory and Factory Method. In InterViews a factory is called kit. The most important kits are WidgetKit and LayoutKit. A widget-kit creates a widget by assembling glyphs according to a concrete look-and-feel. A push-button, for example, is made of a label, two bevels and a mono-glyph that handles the events and invokes the client action. Actions in InterViews are instances of the Command design pattern.
InterViews’ layout semantics is largely borrowed from Donald Knuth’s TEX [Knu84]. It assumes that the space required by a glyph in order to be drawn is rectangular. Each of the rectangle’s dimensions have natural, minimum and maximum sizes. The glyph’s actual space is a matter of negotiation during which the glyph first requests a certain amount of space. After that it will be granted the amount of space it may actually use, based on the requests of other glyphs sharing the same drawing canvas.
The LayoutKit provides factory methods to
All factory methods return a glyph. The tiling methods return a poly-glyph whereas others take a glyph as an argument and return a mono-glyph wrapping the argument glyph.
The ET++ toolkit [WG95] is an object-oriented framework for GUI applications. It is similar to InterViews in that both
ET++ is, however, different to InterViews in that ET++
Two of ET++’s concepts are worth mentioning in this context. One is the notion of bottleneck interfaces and the other one is ET++’s screen update mechanism.
In many cases the interface of a class in object-oriented software can be divided into two sets of methods. These sets can be described as the bottleneck interface and the convenience interface of a class. The methods in the convenience interface are simply front-ends for the methods in the bottleneck interface which do the real work. Overloaded methods are a typical example for that: one of the methods (often the one having the most verbose argument list) is the bottleneck method whereas the other ones are just convenience overloads.
For example, ET++’s VObject (visual object) class has numerous methods to set the origin and size of components: SetExtent(), SetOrigin(), SetContentRect(), SetWidth(), SetHeight(), Align() and Move(). The actual size and origin are altered in SetExtend() and SetOrigin() only. The other mentioned methods all forward to one of these two methods. Hence, SetExtend() and SetOrigin() belong to VObject’s bottleneck interface. In [WG95] the authors say that it “. . . would be bothersome if all these methods had to be overridden in every subclass.” ET++ makes the distinction between bottleneck and convenience methods explicit.
The lack of explicitly documented bottleneck methods has an even worse effect for
the application programmer. Often, the application programmer doesn’t even
know which methods belong to the bottleneck interface. It may turn out to
be hard to figure which methods need to be overridden in application
specific subclasses. Java’s java.awt.Component class serves as a bad
example. It has 10 (!) methods which affect the position and size of a
component.
void move(int x, int y)
void reshape(int x, int y, int width, int height)
void resize(Dimension d)
void resize(int width, int height)
void setBounds(int x, int y, int width, int height) // !
void setBounds(Rectangle r)
void setLocation(int x, int y)
void setLocation(Point p)
void setSize(Dimension d)
void setSize(int width, int height)
Luckily, the JDK comes with the sources to Component, which reveals that all
these methods except one are non-bottleneck methods provided for reasons of
either convenience or compatibility. The only bottleneck method is the first
setBounds overload. Without access to the sources, this can only be determined
by trial and error.
Often, developers of applications and those of frameworks, libraries or toolkits aren’t even aware of the complexity that is introduced by the bottleneck problem. For example, overriding a non-bottleneck method may actually turn out to work as expected in some circumstances. When the application is later extended it may not work anymore because the real bottleneck method gets called and the not the overloaded method. This introduces bugs which are hard to track.
On the other hand, a framework developer might incidentally turn a bottleneck method into a convenience method and vice versa. This may well break existing application code. ET++ demonstrates how this obstacle of inheritance can be avoided by explicitly indicating which methods belong to the bottleneck interface
The authors of ET++ state in [WG95] that application frameworks and class libraries differ in the way they structure the application’s control flow. The user of a class library is required to “. . . know exactly when to call which methods.” A framework, on the other hand, factors out much of the control flow into the framework classes, simplifying the process of writing applications.
Sometimes, factoring out control flow yields cleaner designs and better algorithms too.17 For example, ET++ factors out all of the control flow for the screen update into its view system. That way, redrawing is completely under the control of the redraw system and the update process can be optimized without interfering code of other component classes.
The ET++ update mechanism is asynchronous. The Draw method of components is never called directly. Instead, a component will only be invalidated when it needs to be redrawn due to some change in its internal state. Later, when ET++ is idle, the view system asks all invalidated components to draw themselves. The advantage of asynchronous screen update is that multiple subsequent state changes will not trigger multiple redundant screen updates. The disadvantage is that this scheme does not support animation directly. Animation requires that state changes become visible immediately, i.e. without any noticeable delay.
So far, this paper was focused on toolkits and frameworks implemented in traditional object-oriented languages. I use the term traditional, because they are largely covered by Booch’s definition [Boo94]:
Object oriented programming is a method of implementation in which programs are organized as cooperative collections of objects, each of which represents an instance of some class, and whose classes are all members of a hierarchy of classes united via inheritance relationships.
This section is about SELF ([ABC+95] and [US91]), a mature object-oriented language that does not adhere to the above definition, in that it does not have the concept of classes. Such OO languages are usually referred to as being prototype-based because they use prototypes for object creation, whereas traditional languages use class instantiation.
A language that does not have classes can not offer class inheritance either, raising the question of how such a language supports reuse. Since we are interested in alternatives to inheritance as a concept for software reuse, it is worth having a look at SELF.
Here is a summary of SELF’s important features:
|
SELF can be characterized using two terms: uniformity and minimalism. It is uniform, in that everything is an object and that every object can be used as a prototype for others. Its method lookup unifies closures, methods and objects. SELF is minimal, in that it is untyped, does not differentiate classes and objects, and uses methods for control-flow. It was shown, that SELF can be used to emulate classes without loss in performance. This might indicate that SELF represents the essence of object-oriented languages.
The parent slots of objects are assignable, allowing for dynamic inheritance with the benefit of greater flexibility. It is possible, for instance, to insert a new traits object into an existing inheritance tree at runtime, changing the behaviour of many objects simultaneously. SELF also supports any number of parent slots, thus allowing for multiple inheritance. The method lookup algorithm is even able to handle cycles in the inheritance graph.
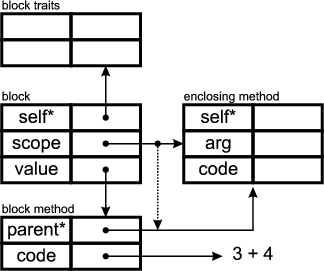
SELF’s ability to pass around lexically scoped code-fragments, i.e. blocks, makes it easy to create callbacks from a framework or toolkit into client code. In Java, for example, something similar can only be achieved by having a non-static inner-class implement a framework defined interface. The Java approach suffers from a much noisier syntax and introduces significant overhead because a Java class is not as light-weight as a SELF-Object. Furthermore, SELF’s blocks have access to the lexically enclosing method’s local slots; it is not possible to access the enclosing method’s local variables from within an inner class.
In section 1.2.2 inheritance was already characterized as an example of white-box software reuse. The opposite is black-box reuse, a term yet to be defined. When a white-box is reused, its inner structure and working principles are subject of exploration and manipulation, making it hard to create new releases of the white-box without breaking existing software that already reuses it. A black-box, on the other hand, only exposes its interface. In [Szy99] object composition and delegation are introduced as approaches to black-box reuse. The book also deals with a the problems that arise when traditional OO-languages are used to implement composition and delegation.
Composition is the technique of combining separate objects (components) into a new object (composite).18 The key idea behind composition is that the resulting capability of the composite is equal or close to the sum of its components’ capabilities. Every component specializes on a particular aspect of the composite’s functionality. The composite uses delegation to dispatch incoming messages to its components. Delegation is similar to forwarding in that both pass the message to one of the components. The lack of a common-self [Szy99], also referred to as object-schizophrenia [CE00], causes problems in combination with simple forwarding of messages. When two classes are composed through inheritance, that is, one class inherits from the other, only one object (an instance of the sub-class) is needed to embody both classes’ functionality. Even functionality included by multiple and transitive inheritance is still represented by one object. However, composition uses multiple objects and every component object has a unique identity.
Consider an object that receives a forwarded message (see figure 1.6). Also assume, that the implementation of that message sends another secondary message which is defined in component and overridden in the composite. One would expect that the overriding method in the composite would receive the message first. Unfortunately, if forwarding is used, the secondary message would be received by the component first. This is because the self of the component is still the implicit receiver. However, if delegation were used, the secondary message would be sent to the composite instead. Thus, delegation has to keep track of two selfs, the composite’s and the component’s self.
The desired behaviour can be implemented in traditional OO languages by instrumenting every method with the additional argument self, which references the current composite. Instead of sending messages to this (as in this.foo() or simply foo()), every component would use self.foo(). Additionally, the composite has to provide dummy methods that forward method calls to the components.
SELF is a language into which composition and delegation are already built-in, and which consequently does not suffer from object-schizophrenia. The composition of objects is formed through the parent slots. The parents are the component, whereas the child is the composite. Delegation is performed by SELF’s method-lookup, which first searches the current object for a matching slot and continues with the current object’s parents, if it did not find one. Furthermore, SELF also has a means for re-sending a message from an overriding method to the overridden one.
SELF demonstrates that OO-languages do not necessarily have to use classes. In SELF there is no distinction between class and object composition. The elegance of this simplified approach also becomes a disadvantage. SELF is dynamically typed, which means that all type checking is done at runtime. The benefit of statically typed programming languages is that the correctness of program can be partially verified by the compiler in an automatic manner.
The authors of SELF claim that the separation of object description and object instance is counter-intuitive and that SELF eliminates this unnecessary complexity. I think that classes are intuitive because they represent how the human mind works anyway: when we think about objects or communicating with others about objects we do not necessarily mean concrete examples of these objects. We treat them as the kinds of objects. According to the SELF authors, class based OO languages cause “meta-regress”: a class is itself an object which needs to be described by another meta-class which is again an object and so on ad infinitum.19
Interestingly, this meta-regress occurs in many areas of computer science. For example, SELF source code is text which describes the initial state and behaviour of a SELF program when it is loaded into the SELF world. This SELF program is a word in the SELF language which is defined by the SELF grammar. In the SELF manual this grammar is specified using EBNF which is, generally speaking, a language itself. The syntax of EBNF can be specified in EBNF itself. This suggests that meta-regress is not counter-intuitive at all - computer scientists and programmers use it all the time.
The observations made in the previous chapter can be summarized as follows:
Consequently, this chapter is about alternative design and implementation techniques which can be used to develop truly reusable object-oriented software. It focuses on the following questions:
As I have shown in the first chapter object-oriented frameworks should employ design patterns and thus focus on the collaboration between objects. This is already true for some of the frameworks and libraries introduced in chapter 1. Nevertheless, it would be ideal if the client programmer could extend the framework to include new patterns and collaborations. Consequently a good framework should be designed based on the notion of pattern-weaving. Pattern-weaving describes the process of incorporating multiple pattern roles into one class.
Figure 2.1 shows an example where three patterns (A, B and C) are woven into four classes: Foo, Bar, Other and Any. Each box stands for an instance of a class. Each pattern in this example consists of two roles. A role is described by an interface, which is depicted by a small circle. Class instances collaborate in a pattern, when their corresponding role-interfaces are connected.
|
|
In the first chapter I have given examples for toolkits in which it is virtually impossible to do that. C++ with its more flexible language constructs like parameterized and multiple inheritance can certainly offer solutions if someone is stuck with a toolkit that needs to be extended. Java, on the other hand, is more limited than C++ and may thus be less future-proof. The common line of reasoning about how Java compensates for multiple inheritance is that in Java interfaces can have more than one parent interface. But Java only provides the composition of interfaces and not that of implementations. So what is needed is a solution for pattern-weaving in Java. The benefit of a pattern-weaving based design is not only that it supports future extension and thus increased reusability - pattern weaving makes easier to understand and maintain software systems because the role interfaces group the aspects of functionality logically.
It is important to note the difference between pattern-based and pattern-weaving-based designs. A pattern-based design consists of design-patterns. A pattern-weaving-based design also allows for later incorporation of other patterns into the design.
Before I decided that a separate tool was needed to achieve a pattern-weaving based design for a graphical editor framework in Java, I experimented with Java interfaces, inner-classes, composition and delegation. Some of the solutions I came up with represent a good compromise for small systems, which is why I would like to introduce them here. The techniques presented are intermediate steps towards the ultimate solution which is introduced at the end of this chapter.
The first solution is a combination of delegation and composition. It defines role interfaces and compositions of role interfaces, i.e. merger interfaces. The composition of interfaces is simply done using interface inheritance; that is, a merger interface extends the role interfaces which it merges. The role and merger interfaces are implemented by role and merger implementation classes. The basic idea behind this scheme is that the merger implementations delegate the work to aggregated instances of role implementations. I would like to explain this in detail using an example which weaves two design patterns.
Figure 2.2 shows the role interfaces for the two patterns to be woven in this example: Composite and Observer. In Chapter 1 I demonstrated that both patterns represent the core of most GUI frameworks. The Composite pattern incorporates two roles: Leaf and Node. Notice that Node is extends Leaf, indicating that a node is a leaf. The roles of the Observer pattern are Subject and View.
__________________________________________________________________________
Specifying roles as interfaces instead of classes is one of the keys to reusable and
extendible software: local variables, method signatures and member variables should not
be declared using names of concrete classes. Java interfaces (or to some extent abstract
classes) are a better alternative. When client and framework code adheres this minor
convention, role implementations can be exchanged without the need to recompile many
other client and framework classes. The only place in which names of concrete classes
must be used is object instantiation. This can be remedied using factory methods or
factory classes, two design-patterns intended to avoid the use of concrete class names for
object instantiation.
__________________________________________________________________________
The empty merger interfaces SubjectLeaf, SubjectNode, ViewLeaf and ViewNode represent valid combinations of the role interfaces.1 Merger interfaces are needed to be able to declare variables2 holding objects which implement multiple roles. A SubjectLeaf, for example, is an object that is a leaf and a subject meaning that it can be a part of a node-object and that it can be viewed. Without the merger interface SubjectLeaf it would be impossible to declare variables holding an implementation of both Subject and Leaf.
Merging the role interfaces seems fairly straight-forward. But interfaces are not very useful if there are no classes implementing them. I would like to start with an explanation about how the merger interfaces are implemented by classes called merger implementations. The implementation of the role interfaces will be described shortly. For now it is sufficient to assume that the role interfaces are implemented by classes called role implementations.
Figure 2.3 extends figure 2.2 with classes implementing the role and the merger interfaces. The role implementations are merged using object composition and delegation. The class SubjectLeafImpl, for example, implements the SubjectLeaf interface by delegating Subject related messages to Subject implementation and Leaf related messages Leaf implementation. References to these role implementations are held in two private member variables; that is, the role implementations are aggregated3 in the merger implementation. Since aggregation is an example of object composition, it is legitimate to say that the merger implementations are composed of role implementations.
Generally speaking, a merger implementation instance aggregates one role implementation instance for every role interface merged by its merger interface. A merger implementation delegates incoming messages to these aggregated role implementations. Note, that there can be any number of implementations for role and for merger interfaces. The aggregation and delegation related functionality is identical in all merger implementations of a particular merger interface. Thus, it makes sense to factor this functionality out and encapsulate it in a base class - the merger base. There is one merger base class per merger interface. All merger implementations of a particular merger interface are sub-classes of this merger base. The merger bases in the example presented here are SubjectLeafImpl, SubjectNodeImpl, ViewLeafImpl and ViewNodeImpl.
Furthermore, the merger implementation base SubjectLeafImpl contains the abstract factory methods createLeaf() and createSubject() which have to be overridden by concrete sub-classes in order to instantiate Subject and Leaf implementations of their choice. The merger base constructor invokes these methods when it needs to create role implementations. Since the merger base contains abstract methods it is itself an abstract class. Consequently, there should to be at least one concrete merger implementation extending the abstract merger base and providing bodies for the abstract factory methods. Alternatively, the factory methods could be non-abstract and return default role implementations.
In the example presented here, all merger interfaces are empty; that is, they do not specify new methods. In some cases, it might be useful to have the merger interfaces specify methods specific to the combination of the role interfaces. These methods, I refer to them as merger methods, should not be implemented by the merger base but by its concrete subclasses.
In the above section I outlined how merger interfaces are implemented by merger implementations which are composed of role implementations. But where do these role implementations come from? Naively speaking, they are just instances of classes implementing the role interfaces. Unfortunately, every delegation-based approach has to cope with object schizophrenia aka. the lack of a common self: in a composite of many objects, each object has its own this. A detailed description can be found in section 1.6.2.
The solution introduced in the previous section deals with object schizophrenia by using Inner... interfaces. Inner-interfaces are extensions of role-interfaces and declare a method called self(). The self() methods is called by merger implementations immediately after the role implementations are created. self() sets the common self reference (Figure 2.4). Role implementations implement this extension interface rather than the mere role interface. Whenever a role implementation needs to refer to “itself” it does not use this but self which is the reference that was passed to the self() method. The following sample code demonstrates that.
By calling self(this) on all aggregated role implementations a merger implementation effectively notifies them that they are now part of a composite. For example, attach() in SubjectImpl does not use this but rather self to register itself with the view. The this reference points to the SubjectImpl instance. The self reference points to the composite i.e. merger implementation.
This solution allows the merger implementation to override a method implemented in the role implementation because every method invocation from inside and outside the composite will be targeted to the common self, i.e. the merger implementation. Without a common self, messages from inside the composite, i.e. from the aggregated role-implementations, would be targeted to the role-implementations themselves and not to the merger implementation. The merger implementation would have the opportunity to catch these messages.
Another advantage of this solution is that Java’s instanceof operator and type casts can be used to test whether an object is a single role implementation or a merger implementation with aggregated role implementations.
If, in the above example, SubjectImpl.attach() used this instead of self for registering with the view, the view would receive a reference to a Subject instead of a reference to SubjectLeaf. Some views might want to specialize in particular subjects like SubjectLeaf or SubjectNode because nodes and leafs might have different representations. The view could use the following code fragment to test whether its subject is a sole Subject implementation, a SubjectLeaf merger implementation or a SubjectNode merger implementation.
class ViewImpl implements InnerView {
... void setSubject( Subject s ) { if( s instanceof SubjectLeaf ) { // code specific to SubjectLeaf objects } else if( s instanceof SubjectNode ) { // code specific to SubjectNode objects } else { // code specific to sole Subject objects } } ... } |
The solution presented here can also be referred to as internal delegation. This is because the delegation happens in the merger implementation. It supports exchangeable role and merger implementations and it deals with object schizophrenia by establishing a common self across the objects in a composite.
Another technique which I want to cover briefly is what I call external delegation. A traditional delegator implements the sum of the interfaces of its delegatees. Consequently, the delegator has to implement every method required by each delegatee interface. All these methods simply forward the call to a delegatee. The delegator essentially exports all its delegatees’ interfaces. The internal delegation solution presented in section 2.1.1 is such a traditional technique. It has the following disadvantages:
The alternative technique presented here removes the burden of forwarding from the delegator.
The outer interfaces Leaf contains
Merger implementations, i.e. delegators, realize (implement) their delegatees’ outer interfaces. Role implementations, i.e. delegatees, each realize one particular inner interface. Unlike traditional delegators, an external delegator only needs to contain one method and one field for each outer interface it implements.
Clients which need to send a message to a delegator instance use this method to
acquire the inner interface implementation to which they then send the
message:
subjectLeaf.leaf().setParent( ... );
subjectLeaf.subject().attach( ... );
This technique is called external delegation, because the forwarding happens in
the client instead of the delegator. External delegation has certain advantages:
it
But there are also drawbacks: external delegation
Like its traditional form, external delegation requires a mechanism providing a common self. To do so, a similar technique to the one introduced on page 60 can be used.
I have shown that delegation can be used to weave design patterns in Java. But it has to be “designed-in”, a term coined by [Szy99]. Whenever a programming language does not directly support a feature (pattern weaving, in this case) as a language idiom it has to be implemented manually using existing idioms. This complicates the design of frameworks and burdens the client programmer as well as the framework author with tasks that should be done automatically. Inheritance is one example of the automated forwarding of messages: the method lookup of object-oriented languages dispatches messages automatically and transparently to the right class in the inheritance chain of an object. Delegation is an alternative technique to inheritance and it may be used to generate more reusable software. But it does so at the cost of extra work on the programmer’s part.
Ideally, a programming language should directly support delegation as one of its idioms. Self, introduced in section 1.6 is such a language. The amount of legacy code written in current languages like Java and C++, will always present an obstacle for alternative languages to become accepted. What is needed is a compromise between native language support of delegation and its manual implementation. The resulting solution should (1) automatically employ delegation and (2) provide a transparent solution for the common self.
The previous section shows that the design of application frameworks involves the process of pattern weaving and how pattern weaving can be achieved using delegation. In this section I will demonstrate that the creation and weaving of design patterns are just incarnations of more general design activities called feature modelling and feature composition. Because feature modelling is a contribution of domain engineering in general and generative programming in particular, both are also covered in this section. The text in this section is a brief (and necessarily incomplete) introduction to Generative Programming based on the material found in [CE00].
Feature modelling is a discipline of domain engineering. The basic idea behind domain engineering is design for reuse. The traditional object-oriented approach assumes that reusability is simply a byproduct of the object-oriented paradigm; that is, if software is object-oriented, it will automatically be reusable. Language idioms like subtype polymorphism (inheritance) and ad-hoc polymorphism (method overloading) are supposed to guarantee future extendibility. Although, it is true that software can be extended using these mechanisms, extendibility is not identical to reuse. Extending software makes it more complex. The complexity grows until it reaches the limit, where it is impossible to maintain, understand and extend the software system anymore.
This situation can only be improved by designing software for reuse. Application frameworks are a well known incarnation of this idea. Their design is targeted towards a family of systems or applications. This family of systems is also referred to as the domain. Domain engineering denotes the process of “collecting, organizing and storing past experience in building systems . . . in the form of reusable assets . . . , as well as providing an adequate means for reusing these assets . . . when building new systems.” [CE00]
According to the above definition, domain engineering consists of three phases: (1) domain analysis, (2) domain design and (3) domain implementation. The purpose of the first phase is to identify the set of application or systems (scoping) and to collect information about this set of systems from customers, experts and other developers. The second phase uses the domain model from the first phase to develop a software architecture shared by all systems in the domain. It identifies the building blocks of the systems as well as their interactions and most importantly their variation across the family of systems.
__________________________________________________________________________
Usually the building blocks of software systems are components or and subsystems. It is
not sufficient to think of subsystems as being made up of subsystems and subsystems as
being made of components. In fact, the component view and the subsystem view are
interleaved: components belong to systems and are made up of other sub-components.
Each of the sub-components belongs to a sub-system and each sub-system realizes a
particular aspect of the component.
__________________________________________________________________________
The result of the domain analysis and domain design is a feature model which is a concise and explicit representation of the variability found in the software systems of the domain. The process of domain analysis and design can be summarized as follows.
The objective of this thesis is the design and implementation of a framework for GUI applications. In chapter 1 several GUI application frameworks were introduced and analyzed. Consequently, the research done for the first chapter is represented by phase 1 and 2 in the above list. Phase 6 is subject of section 2.6 in this chapter. The artifacts of the remaining phases are covered in chapter 3.
The term variability denotes a property’s potential to change from one system of a family to the next. Successfully predicting the variability among the systems of one family is the major goal in feature modelling.
According to [CE00], a feature is an “important property of a concept instance”. A feature model represents the features of a concept as well as their variability. Thus, a feature model represents the intention of a concept. The set of instances described by a feature model is known as the extension of that model.
Feature models are visualized in feature diagrams. There are six elementary types of features:
The features in a feature diagram are represented by nodes in a tree. The root node of the tree represents the concept node. The concept node is connected to its feature nodes through edges. Feature nodes may have sub-feature nodes which are also connected to their parent feature node through edges. Figure 2.5 shows the feature diagram notations for the above types of features.
A mandatory feature is included in the concept instance if its parent feature is included in the concept instance. A optional feature node may be included in the concept instance if its parent is included. If the parent is not included, the optional feature is not included either. If a parent feature with alternative sub-features is included in the concept instance, then exactly one of its sub-features is included. If a parent feature with Or sub-features is included in the concept instance, then any non-empty sub-set of its sub-features is included. Alternative and Or features can be optional meaning that they can be omitted from the concept instance. A feature can also have multiple mandatory sets of alternative and or features.
Features diagrams describe the variability of features. The variability in feature models is represented by the alternative, optional and or feature types. Invariant features are called common features. A features is common if it is always included in the concept instance. All common features are mandatory features, but not all mandatory features are common features. This is because their parent feature may not be mandatory and thus not be included in concept instance. Features with variable sub-features are referred to as variation points.
The variability in feature models requires appropriate variability mechanisms in order to be implemented. Variability mechanisms are also referred to as composition techniques. One of them is single inheritance. Figure shows the implementation of a feature diagram using single inheritance.
Evidently, the implementation of the sub-features S21 and S22 has to be duplicated. Generally speaking, when implementing feature diagrams using single inheritance, duplication can only be avoided if the diagram does not contain any simultaneous, non-singular variation points. Singular and simultaneous variation-points are defined as follows: if a (non-)singular variation point is included in the concept instance, then at most one (more than one) of its sub-features is (are) included. Two or more variation-points are simultaneous if and only if they can be included in the same concept instance and neither is a direct or indirect parent of the others.
If a feature diagram contains simultaneous, non-singular variation points, duplication can only be avoided by using other composition mechanisms like delegation (see section 2.1), parameterized inheritance (see section 2.3), aspect-oriented programming (see section 2.5) and multiple inheritance (see section 2.6).
Domain specific languages (DSL) play a major role in the process of generative programming. Generative programming is an adapted variant of domain engineering which focuses on the automated generation of systems belonging to a particular domain. It is done by generators which are controlled by configuration DSLs. Generally speaking, a DSL “is a specialized, problem-oriented language” [CE00]. It is the contrary of a programming language because it is specific to certain family of systems.
I find the term domain specific language rather vague. In [CE00] TeX and SQL are given as examples for DSLs. Although I understand that both languages are special, problem-oriented languages, I do not see their relationship to domain engineering. Configuration DSL’s, on the other hand, are related to domain engineering. They play an central role in generative programming. A configuration DSL is used to specify the arrangement of a system’s components, i.e. the systems configuration.
“A configuration DSL allows you to specify a concrete instance of a concept, for example, data structure, algorithm, object, and so on. Thus it defines a family of artifacts, just as a feature model does. Indeed, a configuration DSL can be represented as a feature model, and we derive it from the Domain Analysis feature model of a concept by tuning it to the needs of the reuser.” [CE00]
Interestingly, a DSLs does not always have to be created from scratch. There is a special type of DSL called embedded DSL, which makes use of a programming language’s built-in metaprogramming capabilities. For example, the GenVoca (see section 2.3.5) architecture employs C++ static metaprogramming (i.e. templates) to define the composition of systems and components. In GenVoca, the template type expressions (template instantiations and specialization expressions) are the words of the embedded configuration DSL.4
Design patterns are instances of architectural concepts. Why are they only instances of concepts rather than actual concepts? Patterns are concept instances because they are specific to two object-oriented idioms: class composition (interface and implementation inheritance) and object composition (aggregation and association).
The standard text on design patterns [GHJV95] describes each pattern in a consistent format. The description of a pattern starts by explaining its intent, motivation and applicability. This is followed by the structure, the participants, collaborations, implementation and so on. The intent, motivation and applicability are indeed the concept. Its structure is described using object-oriented modelling methods and its implementation is demonstrated using object-oriented languages. This makes the actual pattern a concept instance. For example, the patterns Strategy and Template Method are instances of the concept of varying an algorithm within a family of algorithms. The Observer pattern is an instance of the concept of establishing consistency between representations.
Feature modelling defines the term feature as a property of a concept instance. Consequently, if design patterns are concept instances, they must also have properties, i.e. features. The mandatory features of design patterns are the collaborations between objects. The roles are alternative or optional sub-features of collaborations. For example, the Observer pattern has essentially two collaborations: registration and notification. During registration, the observers (aka views) inform the subject (model) that they want to be consistent with the subject. During notification, one observer modifies the subject and asks it to inform the other observers about this change (see figure 2.7).
Each collaboration defines certain roles. Each object can incorporate multiple roles -- one role per collaboration it is involved in. This means that pattern weaving is just a specialized form of feature composition in which objects are composed of roles. Analogously, objects can be seen as components and roles as aspects of components.
Lately, the object-oriented community discovered, that reuse is not just a automatic side-effect of the object oriented design and implementation of systems. Consequently, the term application framework was coined. Application frameworks are designed to ease and accelerate the development of applications. Applications are software systems. The designer of an application framework focuses on a family of systems. This is were the object-oriented paradigm and domain engineering converge. More reusable software can be created by replacing the OOA/D methods with the methods of domain engineering. But the object-oriented paradigm does not need to be thrown away completely: the idioms of OO-languages can still be used to adequately implement the variation points in domain models.
Selecting a composition mechanism or even creating a new one is the key to a suitable implementation of the variability present in a family of systems. Section 2.1 examines such a dynamic composition mechanism. It also shows that this purely object-oriented approach is not very suitable for the development of larger systems and even families of systems.
Static metaprogramming is another variability mechanism which is why I want to include it in this chapter. Although static metaprogramming cannot be done in the Java language5, static metaprogramming in C++ can give interesting insights. One of them is that feature composition should be done statically, i.e. at compile time. A static composition mechanism for Java will be introduced at the end this chapter. In the beginning of this section I will evaluate static-metaprogramming from a perspective quite different to the perspective of the previous section. At the end of this section (in 2.3.5), I will show how static metaprogramming can be used to implement the feature models introduced in the previous section.
Writing a computer program is often about finding a good trade-off between storage-space and running-time, i.e. between storing state or computing it. State can be stored in the computer’s RAM and disk-drives or it can be computed from other state by the computer’s processing units. Many algorithmic optimization techniques involve the transition from computed to stored state.
__________________________________________________________________________
For example, a binary relation can be implemented as linked list of key-value
pairs. With this implementation the lookup (testing whether the relation is
defined for a certain key) is O(n). A hash-table based implementation has a
slightly better O(max(m,n/B) where m is the average number of keys per
value, n the number of pairs (elements in the relation) and B is the bucket size
(average number of values per hashed key). But the hash-table implementation
uses more memory space than the list implementation. The characteristic
vector implementation which uses the keys to index an array of values has a
lookup of O(n) but needs even more memory because many array items are
unused.6
There are other optimization techniques which do not trade memory space
for running time. If the linked list implementation ensures that the pairs in
the list are sorted in the order of their keys, the lookup can be done using a
binary search which has O(log n). Keeping the list ordered takes additional
time during the operations which insert pairs into the relation and remove
pairs from it. Given a certain distribution among the add, remove and lookup
operations, this extra time is more than amortized by the speedup of the lookup
operation.
__________________________________________________________________________
In the field of language theory and compiler construction the state to be computed and stored is itself a program. The compiler vs. interpreter discussion is basically an example of the space-time tradeoff. A compiler is a program that computes the machine-readable representation of a program based on its human-readable form. The machine-readable program can then be stored, eliminating the need to recompute it every time the program is run. An interpreter, on the other hand, does this computation ’on-the-fly’ while the program is running.
The above mentioned space-time tradeoff in the field of compiler construction has many names: static versus dynamic (binding, typing, optimization), early versus late (binding) or eager versus lazy (evaluation).
C++ templates are an example of a concept which pre-computes state and then stores it. A template is essentially a meta-program; that is, a program about a program. The C++ compiler interprets the meta-program and computes the output program. That’s why this technique is also referred to as static meta-programming. It is called “static” because it is done before the runtime of the actual program. [CE00], inspired by [Vel96], shows how C++ templates can be used to have the compiler compute state that is usually computed by the compilers output program. This technique can yield programs which execute faster because some of their intermediate state has already been pre-computed.
__________________________________________________________________________
There is an interesting parallel between static meta-programming and the ability of
most interpreters to evaluate a string which is computed at runtime and which contains
an expression in the interpreter’s source language. The Perl language, for example, has
the eval construct which can be used to evaluate Perl-code determined at the runtime
of a Perl-program. The Perl interpreter employs a optimization technique common to
interpreters: it pre-compiles the input script into a more efficient binary representation
before executing it. Consequently, the eval function can be used to evaluate
sub-routine definitions. The result of eval on text containing a sub-routine
definition is not the result of the subroutine’s body. Instead it is a reference to the
sub-routine,7
which can then be invoked at the same speed as that of a statically defined sub-routine.
This essentially makes every Perl script a potential meta-program because it has the
ability to generate and evaluate another Perl-program. Often, code consisting of many
conditionals and switch-like constructs can be made more efficient and generic using
eval.
__________________________________________________________________________
The focus of this paper is software reuse. In this section I want to introduce software libraries which have successfully used C++ templates to achieve reuse. It would therefore be useful to have a closer look at C++ templates.
Templates, when examined from the software reuse angle, can be seen as parameterizable software building blocks, i.e. components.8 This is the polymorphic aspect of templates as opposed to the state-computational aspect mentioned earlier. Templates are said to provide static polymorphism. Inheritance, on the other hand, is an example of dynamic polymorphism: a sub-class instance can always be used in place of a super-class instance and the distinction between them is made when a method is invoked, i.e. at runtime. Inheritance and templates are competing techniques regarding polymorphism (see also [BN96]). In the first chapter I have shown that inheritance is not satisfactory in many ways. Thus, templates are interesting because they may lead to a better method of achieving reuse in Java as well.
To be reusable the building blocks have to be generic, that is, they have to be variable regarding some of their features and properties. The more explicit a software building block defines its properties, the more it will limit the possibility of reusing it. To make the template’s properties variable the template will have to be parameterized; that is, all variable properties become parameters of the template. The process during which the C++ compiler automatically makes all of the template’s properties explicit (i.e. substitutes the template’s parameters) is called template instantiation. The template parameters are most likely types.9 Types in C++ are used in many places: classes itself are types, class members (fields and methods) are typed and classes can inherit interface and implementation from other classes by declaring their parent class type. C++ templates can be used to abstract from the concrete types in all of the above-mentioned uses. This has the following consequences:
Another very important consequence is that a class-template’s parent class can be
a template parameter as well. This technique is also referred to as parameterized
inheritance and it shows that templates and inheritance can be used in
combination rather than alternatively.
// template definition
template<class A>
class B : public A {
...
};
...
// template instantiations
B<X> *bx = new B<X>;
B<Y> *by = new B<Y>;
A programmer writing a class that is parameterized by its parent (class B in the
above example) cannot make assumptions about either implementation or
interface of the parent class (A) because it is simply undefined at the time
the template is written and compiled. Thus, the relationship between a
parameterized sub-class and its parent class is less intimate than with explicit
inheritance. Consequently, parameterized inheritance is a good way to inherit
implementation without revealing details about it, that is, to achieve black-box
reuse. It would sometimes be useful to require certain properties of the
parent class parameter, e.g. its interface. The following example illustrates
a hypothetical language extension in which the template parameter A
can only be substituted with a class that extends class X (if X was an
abstract class one would say that A is required to implement the interface
X).
// not C++ !
template<class A : X>
class B : public A {
...
};
...
B<X> *bx = new B<X>;
B<Y> *by = new B<Y>; // illegal, unless Y is a sub-class of X
Constraining the template parameters is also known as bounded polymorphism.
Unfortunately, C++ does not have this feature. GJ, an approved addition to the
Java language standard (see 2.4), allows for this kind of constrained template
parameterization but does not provide parameterized inheritance, and most likely
never will because of the way GJ is implemented.
As mentioned before, parameterized inheritance merges two kinds of polymorphism:
static and dynamic polymorphism. To be more precise, the instance (i.e. a
concrete object) of a class template instance (i.e. a concrete class) with a
parameterized parent class will be subject of dynamic method lookup as
well.
template<class A>
class B : public A { public:
virtual void foo() { A::foo(); }
};
class X { public:
virtual void foo() { printf( "X::foo\n" ); }
};
class Y { public:
virtual void foo() { printf( "Y::foo\n" ); }
};
void main() {
B<X> *bx = new B<X>;
B<Y> *by = new B<Y>;
bx->foo();
by->foo();
}
The class template B in the above example overrides the foo() method. Thus,
B assumes that its base class has a virtual foo() method. Fortunately,
both instantiations of B satisfy this assumption. If, for example, Y didn’t
have a foo() method, the compiler would fail when compiling the B<Y>
instantiation.
The above example shows that I have to adjust my statement that C++ does not provide bounded static polymorphism. In fact, the assumptions made in the class template essentially constrain its instantiations. The only drawback of this is that the constraints are obscure, i.e. not obvious to the programmer using the template.
Another statement which has to be adjusted is the one saying that C++ templates are better suited to black-box reuse. The term black-box implies that to be reused a component does not have to reveal implementation details. Because parameterized inheritance is still inheritance, the template author can make any assumptions about the inherited class. The programmer can, for example, assume that the parent class defines a particular member. The compiler does not enforce the hiding of implementation details. In fact, the compiler cannot verify these assumptions until the template is fully instantiated,10 which means that templates delay the detection of unjustified assumptions and thus weaken type safety. The point here is that a reasonable template author will not burden the template user with justification of assumptions. Instead, a reasonable template author will not make any assumptions at all. As with explicit inheritance, black-box reuse must be achieved with programming discipline rather than support by the compiler. But unlike inheritance, templates do not encourage the programmer to make assumptions about a parent class.
Parameterized inheritance can provide a useful and safer alternative to multiple inheritance. Multiple inheritance introduces hard-to-track ambiguities and every good text book on C++ contains a warning to use it carefully. The following example shows code that uses parameterized inheritance:
This is semantically equivalent code using multiple inheritance:
The pointer assignment in main() of the first example fails. This is because the two compositions A<B<D>> and B<A<D>> have the same interface but are different types. Sometimes this is intentional: if A, B or C contained virtual methods having the same signature (method overriding) and the activation order of those methods was relevant the composition order could be used to define the activation order. However, this feature can cause trouble in cases where there is no semantic difference between the two compositions.
Another issue that deserves attention is code-bloat. Every instantiation of a template will effectively generate a duplicate of the template body. This seems especially unnecessary if the only parameter of a class template is its super class. Code-bloat is often used as an argument against templates. In real-world systems the impact of code-bloat might not be as dramatic. Some of the preconceptions regarding the code-bloat caused by parameterized inheritance are:
Figure 2.8 illustrates the observation made in the last point. The lower left and lower right picture show two single-inheritance alternatives to the design shown in the upper picture. The Shareholder functionality can either be duplicated in the Hired and Long-Term classes or added to the base class of the Employee dimension. Both alternatives have disadvantages. Duplication keeps the base-class and its descendants clean but is hard to maintain. Adding functionality to the base-class can make it overweight (especially if more than two dimensions occur) and pollutes its descendants with unneeded or colliding functionality.
The most important drawback of C++ templates is their limited deployment. Software components are usually either deployed in binary form or as source code. There are several advantages in the binary deployment of components. It provides11
Currently, C++ templates have to be distributed as source code. This is where Java comes in. Because it has a well standardized and simple intermediate binary format for its compiler output, post-compilation composition of classes through inheritance becomes possible. I have written a prototypical tool which implements this and which will be introduced in section 2.6.
Nevertheless, the advantages of static-metaprogramming in C++ as provided by templates are numerous. For scientific computing (number-crunching) for example, template-based approaches to matrix-computation libraries (traditionally a speciality of Fortran) can yield fast and efficient programs. The other standard application of templates are container class libraries.
So far, I have evaluated static-metaprogramming in C++ from a more traditional perspective. This section shows how the GenVoca architecture uses static-metaprogramming to implement feature models. Features models were introduced in section 2.2 as an artifact of the Generative Programming development process, an adapted variant of domain engineering.
Consider the feature model in figure 2.9 which shows an example feature diagram containing the concept node C and its sub-features F1, F2 and F3. Each of the sub-features has sub-features: S11, S21, S22 and so on. F3 is optional and its sub-features are alternative whereas F3 has Or sub-features (see section 2.2.2). I will use this example to demonstrate how a GenVoca architecture can be derived from a feature model and how it can be implemented using static meta-programming.
The procedure which converts the feature diagram into a GenVoca architecture consists of the following steps:
The foundation of the first step is the feature diagram. Each variation-point in the diagram becomes an implementation component. There is an implementation component for each sub-feature, too. Figure 2.10 shows the implementation components of the example.
Components can depend on each other; that is, one component needs to access another component. For example, section 2.2.4 contains the feature model of the Observer pattern (see figure 2.7). It is obvious that the Subject feature depends on the Registrar feature because the subject needs to about know its observers in order to notify them. The Observer feature depends on the Registrant feature in a similar way. Unfortunately, neither dependency is expressed in the feature diagram.
Generally speaking, dependencies between implementation components cannot be made explicit using feature diagrams. Instead, they are a separate part of the feature model and they result from knowledge about the domain. The only way to express component dependencies formally, is to use constraint languages like UML’s object constraint language (OCL). Feature diagrams would be much more useful if they expressed the component dependencies explicitly.
To continue this section’s example, I assume component dependencies as shown in figure 2.11. Component F1 is independent, F2 depends on F1 and F3 depends on F2.
In more complex feature models, there are many components between which no dependency exists. These sets of independent components form component categories. Consequently, component dependencies can be reduced to inter-category dependencies. This section’s example is degenerated in that each component forms a category of its own.
Each component category becomes a layer in the GenVoca architecture. The layers are ordered according to their dependencies. In this section’s example, the category F1 does not depend on any other category. Hence, F1 forms the bottom layer. The other layers are stacked according to their dependencies. The component category of the concept node becomes the topmost layer (figure 2.12).
The comma operator has “or” semantics; that is, any non-empty subset of the set of components separated by commas can be included. The vertical bar operator (|) has “xor” semantics: only one component out of the set of components separated by | can be included.
The GenVoca grammar defines a formal language (set of words) on the set of components plus the set ']', '[' . Each word in the language represents a possible (valid) component configuration or, using feature modelling terminology, a concept instance. The GenVoca grammar can be derived from the layer representation by creating one rule per layer. Each rule has as many | alternatives as there are components in the layer.12
Examples of valid component configurations (i.e. valid words) are c1 = S33[S22[S11]] and c2 = S31[S23[S21[S11]]] and c3 = S23[S11]. The optionality of F3 is denoted in rule (2.1): a word can be produced by using the corresponding rules for either F2 or F3; that is, F3’s layer can be omitted. The Or-semantics of F2’s sub-features is denoted in rule (2.3): it is recursive.
The GenVoca grammar can be implemented using parameterized inheritance. The components are implemented as class-templates. Each class-template is parameterized by its parent class. Parameterized inheritance is subject of section section 2.3 which is why a detailed explanation is not necessary at this point.
The following C++ code shows the class-templates which make up the
implementation of this section’s example.
// layer F1
class S11 {
...
};
// layer F2
template<class PARENT>
class S21 : public PARENT {
...
};
template<class PARENT>
class S22 : public PARENT {
...
};
template<class PARENT>
class S23 : public PARENT {
...
};
// layer F3
template<class PARENT>
class S31 : public PARENT {
...
};
template<class PARENT>
class S32 : public PARENT {
...
};
template<class PARENT>
class S33 : public PARENT {
...
};
// instantiations
typedef S33<S22<S11>> c1;
typedef S31<S23<S21<S11>>> c2;
typedef S23<S11> c3;
The template instantiations at the end of the above sample represent valid component configurations, i.e. concept instances. Each configuration creates an inheritance chain of concrete classes. A concrete class is created by instantiating a template in any of the layers. Instantiating a template in a upper layer creates a class which is derived from a class created by instantiating a lower layer template. Thus, the GenVoca architecture employs configurable class hierarchies.
The above sample code is a very reduced and simplified version of the actual implementation. The difference to real-world examples lies in the lack of any functionality in this example and in fact that an actual implementation of GenVoca using static meta-programming becomes rather complicated. This is mainly due to the fact that C++ templates are more of a language add-on rather than a well integrated language idiom. An in-depth study of GenVoca including real-world examples and their implementation can be found in [CE00].
The recursiveness of rule (2.3) in the example grammar can be used to produce infinitely long component configurations. This is a violation of the original feature model. It violates the Or-semantics of F2’s sub-features (see page 72): if the parent feature of Or’ed sub-features is included in the concept instance, then any non-empty subset of sub-features is included. Sets contain an element once but the grammar rule (2.3) can be used to produce words like: S31[S21[S21[S21[...S21[S11]...]]]] in which S21 occurs more than once.
The grammar can be rewritten in order to correctly represent the Or-semantics of F2. Replacing rule (2.3) with the following rules yields the correct behaviour.
![23 13 12
F2 --> S21[F 2 |F1] |S22[F 2 |F1] |S23[F2 |F1] (2.5)
F223 --> S22[S23[F1]|F1]| S23[S22[F1]|F1] (2.6)
13
F2 --> S21[S23[F1]|F1]| S23[S21[F1]|F1] (2.7)
F212 --> S21[S22[F1]|F1]| S22[S21[F1]|F1] (2.8)](thesis24x.gif)
Although the above grammar is formally correct, its complexity makes it difficult to read, comprehend and implement. Therefore, most GenVoca architectures use the simpler but incorrect grammar and rely on (1) the user or (2) generators to ensure the validity of the configurations. Usually, it is sufficient to trust the user (client programmer) in not creating invalid configurations like S31<S21<S21<S21<S21<S11>>>>>.
Alternatively, generators can be used. A generator is an even more advanced use of static meta-programming. It is a meta-program which is executed by the compiler. It has a loop-construct and a conditional just like normal programs. [CE00] shows how a static C++ meta-program can be used to have the compiler parse a configuration DSL (see section 2.2.3) and generate a valid configuration.
The major benefits in using a GenVoca architecture are flexibility and efficiency. GenVoca is flexible since it allows for a large number of different component configurations. Despite this a GenVoca architecture yields highly effective code. Traditional object-oriented programs spend much of their run-time by repeatedly performing redundant activity like virtual method lookup. GenVoca moves much of this activity to compile time.
Obviously, GenVoca’s flexibility is the foundation of reusability. Furthermore, GenVoca allows the client programmer to add her own application-specific layers. This is because it is the client programmer who creates the configurations. In traditional object-oriented designs, the configurations are “hardwired” into the class hierarchy.
The disadvantage of GenVoca is the complexity of its implementation. Templates are difficult to comprehend for unexperienced programmers as is the whole concept of static-metaprogramming. Furthermore, a GenVoca architecture introduces subtle dependencies between class templates in different layers. I have never implemented a GenVoca architecture myself, but I suspect that it is not easy to interpret the error messages emitted by a C++ compiler when it encounters an invalid component configuration.
This section is a compact introduction into Generic Java (GJ). GJ is a source and binary compatible Java compiler which adds one idiom: parametric polymorphism. The name Generic Java results from generics or generic types -- a synonym for parametric types. Generics are not another variability mechanism, an important subject of this thesis. The reason for including GJ in this text is that GJ, unlike C++, supports bounded type parameters. GJ is a result of the efforts related to parametric types in Pizza, another experimental Java compiler. More material about GJ can be found in [BOSW98a] and [BOSW98b].
To explain how GJ works it is best to look at an example. The following sample code illustrates GJ’s usage for a singly linked list container. The sample only includes two operations: add() which adds an element to the end of the list and last() which returns the last element. The other operations are omitted.
The most notable difference between GJ source and standard Java source is the
appearance of type parameters denoted by angle brackets. For example, the class
List is parameterized by the type of objects it contains. The place-holder for this
type is A. The list can later be used to hold any type of non-primitive objects. A
list of strings is created as follows:
List<String> list = new List<String>();
list.add( "Hello, world!" );
String string = list.last();
If the list was implemented in standard Java without parameterized types, the
above code would look like this:
List list = new List();
list.add( "Hello, world!" );
String string = (String) list.last();
The cast in the last line of the example is necessary because in a standard
implementation, the operation last() returns an object of type Object -
the most general object type. A non-GJ implementation of List would
also use Object-typed variables to reference the stored user objects. The
non-GJ list can be used to hold any non-primitive object type, just like the
GJ list. But it does so at the cost of sacrificing type-safety. At compile
time, the programmer is not protected from adding apples to the list
and accidentally trying to retrieve oranges. The non-GJ list is effectively
untyped.
This is not only the case in our simple example: all container classes in Java’s built-in util package use Object-typed references to receive, store and return user objects. They are all untyped.
Using GJ eliminates the type-cast. This makes the client code type-safe and easier
to read. A List<String> can only be used to hold strings. Trying to add
something else results in a compile time error. For example, it would be
impossible to add Apple objects to a List<Orange>. A list that holds apples and
oranges can be created by making Apple and Orange extend the same
super-class13
and instantiating the list type using this super-class:
class Fruit { ... }
class Apple extends Fruit { ... }
class Orange extends Fruit { ... }
List<Fruit> list = new List<Fruit>();
list.add( new Apple() );
Fruit fruit = list.last();
if( fruit instanceof Apple ) {
... (Apple)fruit
} else if( fruit instanceof Orange ) {
... (Orange)fruit
}
How does GJ work? According to [BOSW98b], the approaches to implement generic, i.e. parameterized types can be divided in two categories. GJ employs a homogeneous approach whereas C++ and Ada use a heterogeneous one. The heterogeneous solution duplicates the code in a class template for every template instantiation.
The homogeneous approach used by GJ replaces every occurrence of a type place-holder (<A> in the above example) with the type Object.14 This can be verified by decompiling the byte-code generated by GJ for the above List implementation. For example, the method last() becomes
Object last() ...
and
String string = list.last() );
becomes
String string = (String) list.last() );
More precisely, GJ replaces type parameters with Object in generic type definitions. GJ inserts cast from Object to the concrete type whenever an instance of the parameterized type is used. This novel type algorithm is called erasure.
GJ’s working principles are more sophisticated than described here. GJ features parameterized classes as well as parameterized methods. GJ integrates Java’s subtype concept for classes and it supports mixing legacy code with code that uses generic types.
A disadvantage of the homogeneous approach is that it doesn’t allow for parameterized inheritance; that is, sole type parameters may not occur in the extends clause of classes and interfaces. The erasure algorithm only works for the use of generic types in method signatures and variable declarations. The following code is rejected by the GJ compiler: class Foo<A> extends A { ... } On the other hand, instantiations of generic types may occur in the extends clause: class Foo<A> extends Bar<A> { ... } Therefore, GJ’s generic types cannot be used as a composition mechanism in order to implement the feature models introduced in section 2.2.2. Nevertheless, GJ represents major improvement of the Java language. In the course of the Java Community Process, GJ has been proposed and accepted as a future addition to the Java language standard.
In C++ type parameters of templates accept any concrete type. There is no way
to restrict the set of types a template can be instantiated with. GJ uses
subtype polymorphism to confine type parameters. The following example
defines the interface Comparable and the class Set. In order to speed
up the lookup operation (binary search), Set keeps its elements sorted
internally
interface Comparable {
int compareTo( Comparable that );
}
class Set<A implements Comparable> {
boolean contains( A a ) {
...
if( 0 == a.compareTo( b ) )
...
}
}
The elements can only be sorted if they can be compared against each other.
Therefore, Set restricts the type parameter A to classes implementing the
Comparable interface. Generally speaking, if a type parameter of a generic type is
bounded, it can only be instantiated using subtypes of the parameter
bound.
Consequently, the erasure algorithm mentioned earlier only replaces the
occurrence of unbounded type parameters with Object. The erasure of bounded
type parameters is their bound. In other words, if no bounds are specified,
Object is the bound. The erasure of the above example yields the following
code:
class Set {
boolean contains( Comparable a ) {
...
if( 0 == a.compareTo( b ) )
...
}
}
A hypothetical compiler supporting a combination of bounded parametric
polymorphism and parameterized inheritance would be a superb mechanism to
implement a GenVoca architecture. I refer to this combination as bounded
parameterized inheritance. It is obvious that GenVoca can only be realized
with parameterized inheritance, since inheritance is used to “wire” the
components across the GenVoca layers. But GenVoca also introduces
dependencies between the components. For example, a upper layer component
may invoke a method of a lower layer component. What if the author
of the upper layer is different to the author of the lower layer? What
if the lower layer’s author changes the signature of the method? These
problems can be managed by confining the component template parameters.
In order to explain how this might work, I would like to reanimate the
example of section 2.3.5 on page 97. The following Java-like sample code
shows how this example might look like with bounded parameterized
inheritance:
// layer F1
interface F1 {
void foo();
...
}
class S21 implements F1 {
...
}
// layer F2
interface F2 {
void bar();
...
}
class S21<PARENT implements F1>
extends PARENT
implements F2 {
...
void bar() {
foo();
}
...
}
...
Each layer in the above example defines its own inter-layer protocol in the form of an interface. All components in a particular layer implement this protocol. The protocol interfaces are named after the layers which are in turn named after the corresponding variation points in the feature diagram (figure 2.9).
Using bounded parameterized inheritance has a significant advantage: the check whether all components are in accordance to their layer protocols can be done when compiling the components. In traditional GenVoca this check is done when the components are configured. This difference is important: the components are usually compiled by the provider of the components but they are configured by the client or application programmer.
Inter-layer protocols make the dependencies between components in different layers explicit. They improve the comprehensibility and soundness of a GenVoca software system.
Aspect-oriented programming (AOP) is a relatively young programming paradigm proposed by the researchers at Xerox PARC. The development of AOP was inspired by the observation that every software system has to handle more than one issue simultaneously and that only a subset of these issues can be organized as a hierarchical composition of modular units, e.g. methods, function, procedures, objects or modules. The remaining issues crosscut the units in which this subset of main issues is organized.
This section reviews AOP as a composition mechanism in general and a mechanism to weave design patterns in particular.
The principle of separation of concerns was coined in 1970 by Dijkstra. It formalizes what humans instinctively do when they deal with complex matters: focus on one issue at a time. Applying this principle to programming means to organize a program into smaller modular units which are made up of even smaller sub-units. Each of the units is specialized in dealing with one particular program aspect.
Ideally, during the implementation of a unit, the programmer does not need to think about the whole program. Instead, he or she can focus on writing the unit. Another advantage is that the work on a system can be distributed among many, more or less independently working programmers; that is, separation of concerns enables the collaborative development of software. Yet another advantage is that the units of one software system might be reused for another software system. This is what separation of concerns claims. A software developer’s reality may look different:
A programmer instinctively maps the predominant aspectual dimension onto this single compositional dimension. The aspects in subordinate dimensions will crosscut the units in the predominant dimension. This means that the implementation of subordinate aspects is fragmented and that the fragments are scattered across the units. Worse than that, a fragment has to be duplicated if it occurs in multiple units.
If the subordinate aspects of the old system are not needed in the new system, the old system’s units can not be reused for the new system because they contain superfluous fragments. The same happens if the new system introduces subordinate aspects not present in the old system.
What are aspects? Were and how do they occur? The following examples answer these questions.
The main task of a web-server15 is to receive HTTP object requests from clients (e.g. web browsers), perform the necessary actions to retrieve the object locally and send the object back to the client. Other main tasks include the processing of configuration files, managing a memory cache of objects, managing client connections, encryption and server side scripting. These tasks are the predominant aspects of a web-server. In a object-oriented design, these aspects are encapsulated in units like packages, modules and classes. In a good object-oriented web-server design, these units can be reused for servers of other Internet protocols and other kinds of servers like HTTP-proxies.
Besides these predominant aspects of a web-server there are also subordinate aspects like logging and failure handling. Both aspects are implemented in the form of duplicated code fragments scattered across the system’s unit. Logging is used to trace the behaviour of non-interactive programs like server daemons. In every important method of every class in every package there will be at least one line of code devoted to add an entry to the log.
__________________________________________________________________________
The past has shown that no program, besides TeX of course, is fully correct.
Correctness in this context means that the program has predefined behaviour under all
conditions and for all sorts of input. As the complexity of software systems grows it
becomes inherently difficult to accurately predict their behaviour. In other words, it is
very likely that the system fails under certain conditions. The term robustness describes
the quality of a software system to handle its own failure. Robust software adds extra
code to assert important invariants, to check the results of method invocations
and to react gracefully in case these assertions and checks fail. Like logging,
this failure handling code fragments are duplicated and scattered across many
methods.
__________________________________________________________________________
A purpose of a list container is to hold user objects such that the order, in which the objects are added to the list, is retained. There are other properties of lists like morphology (whether the elements all need to have the same type or whether different types are allowed) and bounds (fixed or variable size). All of the above properties are the predominant aspects of lists. It is possible to implement these aspects using a traditional class hierarchy.
Another property of lists is synchronization, i.e. whether a list is thread-safe. A list can be made thread-safe by wrapping its methods with code that serializes access to the list’s internal data-structure. Java has the appropriate synchronization mechanism built-in. The easiest way to synchronize a list in Java is to a method synchronized if it accesses the list’s internal data-structure. A method is synchronized by simply adding the keyword synchronized to its signature. When the Java compiler finds a synchronized method, it generates special wrapping code around the body of the method. The wrapping code uses the current object (this) as a mutex in order to serialize the execution of the method body. As a result only one thread at a time can execute any of the synchronized methods for a particular object. Obviously, this serialization code induces additional run-time overhead. For lists which are accessed by only one thread, this overhead is redundant. Consequently, a good list container design should distinguish between lists that are synchronized and lists that are not. It is therefore not an option to simply add the synchronized statement to every method in every class in the list hierarchy. Synchronization becomes a subordinate aspect of lists.
The designers of the new Java container (i.e. collections) class library were aware of the synchronization overhead. They chose the Decorator pattern to achieve the distinction between synchronized and unsynchronized container classes. All container implementations are unsynchronized by default. In order to make a unsynchronized container synchronized, one calls a factory method in Collections. For example, the factory method synchronizedList() in the following sample code creates a synchronized list by decorating (wrapping) the argument list with list synchronized implementation. The synchronized list implementation does nothing but synchronizing on a mutex object and forwarding to the wrapped list.
The downside of this approach is that it needs one additional decorator class per container class. The methods in the decorators look all the same. Writing decorator classes is definitely a tedious task. It is something that should be automatized. Aspect-oriented programming does exactly that.
The basic idea behind AOP is to encapsulate aspects in a new type of modular unit and to provide means to selectively distribute and merge these units with the other predominant units in an automated way. How this works is best explained using a concrete AOP implementation: AspectJ.
AspectJ is an aspect oriented language extension for Java. It is also a collection of tools including the compiler ajc and a debugger ajdb. The AspectJ compiler is Java compatible in that it accepts standard Java source files and produces standard Java class files. Besides that, the compiler also accepts source files in extended AspectJ syntax. It is implemented as a front-end for javac -- the Java compiler that comes with Sun’s JDK. The AspectJ compiler parses the source files, transforms them into standard source files and passes the transformed Java source to javac which generates the class files.
The extended aspect-oriented syntax introduced by AspectJ centers around the aspect keyword. In analogy to the class keyword which encapsulates the description of object behaviour and state, the aspect keyword encapsulates the description of aspects.
Here is an example aspect description for the synchronization aspect of Java2’s container classes mentioned on page 124.
Line 1 states that this source and everything in it belongs to the package java.util -- the package which contains Java2’s collection classes. Line 4 defines a new aspect named SynchronizedCollection1.
Line 06 introduces a mutex member to every class being a subtype of AbstractCollection from which every collection class in java.util is derived. The statement on line 6 is an introduction. An introduction can be used to add methods and fields to classes and interfaces. As a result of line 6, the AspectJ compiler scans for all sub-classes of AbstractCollection and adds the mutex field to them. The mutex field will be initialized with an instance of Object (line 7).
The statement on lines 9 to 11 declares a point-cut named publicMethods. Simply speaking, a point-cut is a well-defined set of locations (aka join-points in AspectJ terminology) in the control flow of a program. The fact that the point-cut is parameterized is not important here. The important thing happens on line 10 and 11. Line 11 matches the body of public methods of any name, having any return type and any argument. Line 10 constrains this set further to the set of public methods which are instances of subclasses of AbstractCollection. In other words, the point-cut on lines 9 to 11 defines a set of join-points named publicMethods which includes the bodies of all public methods in sub-classes of AbstractCollection.
The statement on lines 13 to 18 declares an advice. An advice is a code fragment which is to be added before, after or around the join-points (control flow locations) in a point-cut. The advice on line 13 is an around advice. Again, for certain unimportant reasons, the advice is parameterized. On line 14 the advice refers to the point-cut defined on line 9. The body of the advice contains a block which synchronizes on mutex. Inside the synchronized block the special function proceed() is called which is simply a place-holder for the original join-point around which the advice is put. The expression c.mutex on line 15 refers to c which stands for an instance of AbstractCollection. c.mutex accesses the mutex field of this instance. Where does this field come from? Remember, that on line 6 a field named mutex was added to every subclass of AbstractCollection.
When the classes in java.util package are compiled in conjunction with the above aspect, every public method of every collection class in that package will be wrapped with synchronization code. The subordinate aspect SynchronizedCollection1 is now woven into the system. This is very close to what is intended. Unfortunately, the original aspect-unaffected classes do not exist anymore. The AspectJ compiler does not allow to have both, aspect-affected and aspect-unaffected classes in a single system. The decision whether the collection classes are synchronized or not has to be made at compile time. This is demonstrated below in a second version of the synchronization aspect.
The following version of the synchronized aspect allows synchronized and unsynchronized collections to co-exist in the same program:
The main difference to the previous version of this aspect is that SynchronizedCollection2 is not a singleton anymore. Instead, each synchronized instance of a container class is bound to an instance of this aspect. Aspects can be instantiated because AspectJ translates aspects into normal classes. The eachobject modifier on line 5 to 7 binds an instance of this aspect to every instance of a subclass of AbstractCollection on which the synchronize() method has been called. The binding will be established when synchronize() is called. This method is added to every AbstractCollection subclass by the introduction on line 10. The mutex field is now a member of the aspect (line 12). The point-cut on line 14 excludes the synchronize() method (line 17).
This has the effect that every public method has to check whether the current collection instance is synchronized. A synchronized collection instance is bound to (i.e. associated with) an instance of the SynchronizedCollection2 aspect. The association is established when the synchronize() method is called.16 Depending on whether the collection instance is synchronized or not, every public method in the collection class either executes synchronized or unsynchronized code.
class List extends AbstractCollection {
public void add( ... ) { SynchronizedCollection2 aspect = SynchronizedCollection2.aspectOf( this ); if( aspect != null ) { synchronized( aspect.mutex ) { orig_add(); } } else { orig_add( ... ); } } public void orig_add( ... ) { ... } } |
AspectJ provides much more control about selecting join-points than can be described here. Possible join-points include locations in the code where a method is called, where an exception is thrown. Besides the around advice, there are the advices before and after. An introduction can also make a class extend a different class or implement another interface. I have shown that aspects can be instantiated once per JVM (singleton aspect) and once per object. Furthermore, there can be an aspect instance per control-flow.
AspectJ allows aspects to extend classes. This is useful for eachobject aspects like version 2 of the synchronized collection aspect. Note, that AspectJ translates each aspect into a Java class. If an aspect A extends a class C, AspectJ will translate this aspect A into a class A' which extends class C.
Aspects can also be abstract; that is, some or all of its point-cuts may be abstract, i.e. declared but not yet defined. The abstract point-cuts may be referred to by the abstract aspect’s advises. Aspects can extend abstract aspects and define the inherited abstract point-cuts. Aspects may not extend concrete aspects. Neither may classes extend aspects.
The similarity between aspects and features is striking. Features are important properties of concept instances and aspects are properties of instances of language constructs like classes and methods. At the design level, features and aspects are synonymous terms. The important difference between aspects and features is that aspects are not only a design paradigm but also an implementation mechanism.
This suggests that aspects can be used as a variability mechanism for the implementation of feature models. The synchronized list example on page 126 demonstrates the implementation of very simple feature diagrams. The feature diagrams for version 1 and 2 of that example are shown in figure 2.13. Both diagrams are overly simplified in that the Storage feature is in fact the parent node of a complex tree of sub-features. This feature tree is needed to classify the different types of collections (set, bag, map, list).
|
|
I do not want to give a complete description of how aspect-oriented programming can be used to implement feature models because of two reasons.
The last point can be illustrated using the above example. The only difference between figure 2.13a and b is the optionality of the synchronization feature. If synchronization is modelled as an optional feature, the optionality is decided at runtime; that is, every method of a collection has to check whether the collection object is synchronized or not and execute the appropriate code. Usually, a collection instance will either be synchronized or unsynchronized an remain so until it is garbage collected. It is very unlikely that an application requires a collection to become synchronized in the middle of its lifetime. Hence, the optional synchronization feature should be resolved statically.
This does not only apply synchronization -- most variation points in a software system can and should be resolved statically. Currently AspectJ leaves developers two alternatives: either all collection classes are (un)synchronized (static mandatory feature) or synchronization is decided at the object level (dynamic optional feature). If AspectJ included a mechanism for retaining the aspect-unaffected classes, the optionality could be decided at compile-time.
On the other hand, AspectJ has promising potential to be used for feature model implementations. Section 2.2.2 shows that feature models can be implemented using single inheritance but that this induces duplication except in the (unlikely) case that the diagram does not contain simultaneous non-singular variation points. Duplication is only problematic if it has to be carried out manually by the programmers. AspectJ can be used to automatize duplication if simultaneous non-singular variation points are implemented as aspects (figure 2.14).
AspectJ tries to be in-line with traditional Java syntax. This is more confusing than helpful. For example, the parameterization of point-cuts and advices looks particularly strange: pointcut p( AbstractClass c ) : instanceof( c ) ... The parameter c looks like a normal variable of type AbstractClass. On the other hand, it is passed to the instanceof designator which makes it a type name.
Aspect-oriented programming can be achieved by either a creating a new language or by extending an existing language, i.e. as an language add-on. AspectJ is an instance of the latter. Probably, the most important drawback of this approach is that it requires sophisticated and expressive means to systematically dissect the constructs of the original language. Casually speaking, a lot of thought has to be invested in taking apart what should be separate in the first place.
AspectJ treats aspects as first-class citizens. This decision has disadvantages:
Nevertheless, AspectJ provides powerful mechanisms for the management of large existing object-oriented software systems.
In this section I will describe the concept, design and some implementation issues of the WeaveJ prototype which I developed during the research for this text. Generally speaking, WeaveJ is a tool for class composition and it is mainly intended for pattern weaving. It lets developers focus on the patterns they want to use in their software instead of forcing them to think about how these patterns can be woven.
Pattern weaving, on the other hand, is just an incarnation of feature modelling and generative programming (section 2.2). When seen from a feature modelling perspective, WeaveJ is a variability mechanism similar to multiple inheritance. Since Java does not support multiple inheritance, WeaveJ simulates it by serializing the multiplicity. Once a serialized form of the multiple inheritance graph is found, WeaveJ composes the classes using single inheritance.
But WeaveJ is not just “multiple-inheritance for Java”. WeaveJ delays the composition of classes until the final application is compiled. Hence, the application programmer has complete control over the composition process. Framework classes can be extended or replaced by the application programmer at any location in the inheritance hierarchy -- not just at the leafs. This is an important advantage over traditional multiple inheritance, where the inheritance relation between framework classes is fixed and cannot be influenced by the application programmer.
WeaveJ’s composition granularity is not as fine as, say, AspectJ’s. WeaveJ only supports composition at the class level. Roughly speaking, AspectJ composes at the intra-method level. I claim that using WeaveJ makes this level of composition granularity obsolete because WeaveJ also represents a new approach to framework design. AspectJ is a implementation technique which does not really introduce new concepts into the design of software. Aspect-oriented programming gives the impression that it is intended to make up for problems that should actually be fixed at the design-level. The object-oriented paradigm is powerful enough to provide truly reusable software under the assumption that the inheritance relation between classes is managed in a less static way. WeaveJ encourages this new design approach. It employs Java interfaces to specify aspects of objects. It uses classes to implement these aspects and it uses inheritance to compose these aspects into a composite object.
WeaveJ is written in and for Java. It is a post-compilation tool, which means that it is for use after compilation. It is used by both, the framework provider/maintainer and the framework user, i.e. application/client programmer. WeaveJ adheres to the component-oriented paradigm (COP, see [Szy99]). It maps COP to OOP by employing classes as components and composing them with inheritance.
WeaveJ’s working principle is best explained using a simple example. The feature diagram in figure 2.15a shows a concept with three or-features. According to the definition in section 2.2.2, any non empty subset of the set {F1,F2,F3} can be included in concept instances of C. Figure 2.15b shows a complete implementation of this feature model using multiple inheritance.
|
a)
|
Assuming that there is only F123, neglecting the existence of F12, F23 and F13, it does not really make a difference to F123 if it inherits the necessary functionality by multiple inheritance or in a serialized chain of single inheritance as shown in figure 2.15c. WeaveJ uses this effect to simulate multiple inheritance. Taking F12, F23 and F13 into account again, only requires that certain classes have to be duplicated in order to avoid conflicts. This is explained in section 2.6.3.
The single inheritance chain in figure 2.15c is very similar to the configurable inheritance hierarchies in GenVoca architectures. In GenVoca, each concept instance is represented by a chain of components -- one component per layer. Upper layer components are derived from lower layer components. WeaveJ represents a hybrid between GenVoca (parameterized inheritance) and multiple inheritance: feature models can be implemented as if multiple inheritance was available but WeaveJ converts these model implementations to single inheritance hierarchies like the ones in a GenVoca architecture.
The good news for Java programmer using WeaveJ is that they can now develop their programs as if Java supported multiple inheritance. WeaveJ will transparently simulate multiple inheritance using single inheritance. The generated programs will run on any Java2 compatible virtual machine.
The WeaveJ tool is pure Java, meaning that it is written in Java and can only be fed Java. WeaveJ does operates on the byte-code rather than the source-code. This means that its input and output are class-files. I was able to implement the WeaveJ in only three weeks, thanks to Java’s well defined class-file format and the availability of several byte-code engineering libraries. It still has certain insufficiencies which will be analyzed at the end of this section. Thus, WeaveJ in its current revision is definitely prototypical. Despite this, it can be used to verify the feasibility and benefits of this variability mechanism.
Terminology remark: When using the term interface in this section I am referring to the Java meaning of interface. The term implementation refers to a Java class implementing a particular Java interface. The terms component and composite are used according to their COP definition. Their use in this section is not related to the Composite design pattern.
For interfaces, Java supports multiple inheritance. Consequently, the implementation of a feature model in WeaveJ is specified using interfaces. This is the first phase of the WeaveJ process -- based on the feature model, the programmer creates an inheritance graph made up of interfaces.
The second phase is writing appropriate classes which implement the interfaces defined in the first step. A class implementing a particular interface can assume that the methods in the parent interfaces are available and it only needs to implement the methods required by its own interface. There can be any number of alternative classes implementing a particular interface. Only one implementation will occur in the final application. The application represents a concept instance.
The third phase is the specification of the binding file. For every interface, the binding file specifies one implementation class. Only the specified class is included in the application. The binding mechanism will be dealt with in detail in section 2.6.5.
The fourth phase is building the application. The programmer uses the Java compiler to translate the source code of all implementation classes into class files. The WeaveJ tool is then used to compose the compiled byte-code representations of all implementation classes in a single inheritance chain, simulating the interface inheritance graph created in the first phase.
From now on, the feature modelling terminology will not be used anymore. I will refer to interfaces with parent interfaces as composites. Interfaces without parent interfaces are called components. A class which implements one of these interfaces is referred to as composite implementation or component specification respectively.
The next section introduces a simplified graphical notation for class diagrams. These diagrams contain composition graphs and the visualize class and interfaces as boxes. As in UML, interface and class inheritance is symbolized by arrows with empty heads. The realizes relation (implements in Java) between classes and interfaces is not denoted graphically but textually, e.g. “Aimpl implements A”. If there is more than one implementation of a particular interface, the classes will be numbered as in “Aimpl1, A impl2 . . . ”.
Serialization17 is the algorithm used by WeaveJ in order to simulate multiple inheritance. For any class, it does not matter whether it inherits from all its base classes at once or from only one base class which inherits from the second which inherits from the third and so on.
On the left side of figure 2.16 a more complex composition graph is shown. C, E,
I, J and K are composite interfaces. K and J are composites consisting of other
composites. The corresponding Java source skeleton is as follows.
// the interfaces:
interface K extends C, J;
interface C extends A, B;
interface J extends E, I;
interface E extends D;
interface I extends F, G, H;
// the components
class AImpl implements A;
class BImpl implements B;
...
class KImpl implements K;
Note that there can be many classes implementing a particular interface. WeaveJ
selects one of these implementations based on the current bindings, a mechanism
that will be explained later in this section.
The goal of serialization is to produce an inheritance graph with at most one
parent per class (single-inheritance graph). This is because Java only supports
single implementation inheritance. The result of serializing the above example can
be described using the following Java sample code.
class BImpl extends AImpl;
class CImpl extends BImpl;
...
class KImpl extends JImpl;
Obviously, the single-inheritance graph represents just one of the many
total orders which satisfy the partial order defined by the original graph.
Formally speaking, there is only one constraint on the order of classes in the
single-inheritance graph:
Let B be an interface which directly or indirectly inherits the
interface A (A  B). In the resulting single-inheritance graph B’s
implementation must occur after A’s; that is, A’s implementation
must directly or indirectly inherit B’s (Aimpl
B). In the resulting single-inheritance graph B’s
implementation must occur after A’s; that is, A’s implementation
must directly or indirectly inherit B’s (Aimpl  Bimpl).
Bimpl).
The order shown on the right side of figure 2.16 is the post-order of the graph to its left. The post-order can easily be computed by doing a recursive depth-first traversal on the graph. Upon return from each level of recursion the current node is appended to the end of a list. When returning from the starting node (K in the above example), the list holds the graph’s post-order. Note that if the given graph defines an order on the outgoing edges of each node it will only have one post-order.
Another possible total-order besides the post-order is
 B
B  D
D  F
F  G
G  H
H  C
C  E
E  I
I  J
J  K
KThe examples presented so far are special since their composition graph degenerates to a tree. WeaveJ can handle the more general single-rooted directed acyclic graphs like the one shown in figure 2.17. Here, interface F is inherited by two interfaces: E and I. Obviously, the post-order still satisfies the above constraint because multiply inherited interfaces and their ancestors might be appended earlier but never later. Consequently, they only move towards the beginning, i.e. get smaller. In order to violate the constraint, an interface would have to be appended later such that it moved towards the end of the list thus bypassing one of its descendants.
The above examples only deal with one composite graph at a time. Clearly,
frameworks can comprise any number of composites. The resulting composition
graph is not necessarily single-rooted any more. To be able to produce a
serialization, WeaveJ treats each composite independently. Each composite defines
its unique single-rooted composition subgraph. The example illustrated in
figure 2.18 has two composites C and E. Both inherit the component B.
Unfortunately, Bimpl appears in the middle of both post-orders to the effect that
two versions of Bimpl are needed: Bimpl1  A
impl and Bimpl2
A
impl and Bimpl2  D
impl.
D
impl.
|
|
If the subgraphs looked like figure 2.19 with B at the beginning of each post-order, then both post-orders would be able to share B. The only difference between figures 2.18 and 2.19 is the changed order of the outgoing edges of C and D. This means that the order in which edges will be traversed during recursion is very important.
Duplication becomes even more significant when the duplicated component has
ancestors, as shown in figure 2.20. In this case all ancestors have to be duplicated
as well. This is because Fimpl needs to be duplicated (Fimpl1  A
impl and
Fimpl2
A
impl and
Fimpl2  D
impl) which in turn causes B to be duplicated (Bimpl1
D
impl) which in turn causes B to be duplicated (Bimpl1  F
impl1 and
Bimpl2
F
impl1 and
Bimpl2  F
impl2). The current WeaveJ prototype does not make any provisions to
minimize class duplication. Such optimization would have to select the best
configuration based on, for example, the number of duplicated classes or their
sizes.
F
impl2). The current WeaveJ prototype does not make any provisions to
minimize class duplication. Such optimization would have to select the best
configuration based on, for example, the number of duplicated classes or their
sizes.
Using parameterized inheritance for GenVoca architectures causes duplication of code (see also section 2.3.4). Using AspectJ to implement feature models induces code duplication, too. But both kinds of duplication are not problematic because they are carried out automatically by the compiler. The same applies to WeaveJ: the classes are duplicated without bothering the programmer. Duplication in WeaveJ is invisible to the programmer with the exception of the increase in code size.
As shown in previous sections, an alternative to inheritance does not necessarily need to abandon it. Consequently, WeaveJ does support inheritance between implementations. This is best illustrated using an example (see figure 2.21).
|
|
Usually, atomic implementations, i.e. implementations of non-composite interfaces, do not have a parent class.18 This is because WeaveJ encourages a framework design based on composition instead of inheritance. However, in some situations it might be convenient to allow the client programmer to extend or override functionality provided by one of the framework’s components; that is, implementations.
If, for example, the framework component is buggy and needs to be fixed, the client programmer has to replace it with a custom implementation. Often, the custom implementation differs from the component it replaces only in minor details. This suggests that the custom implementation inherit the framework component. Figure 2.21 shows that B2impl extends Bimpl and that B is bound to B2impl. In order to support inheritance between implementations, WeaveJ’s serialization algorithm only needs to include all ancestors of an implementation (Bimpl in this example).
This form of inheritance can be useful in other situations too. Suppose that a component’s activity must be monitored in order to debug it. This could easily be accomplished by extending this component through inheritance and wrapping every method in the inheriting component with logging code.
As was described in previous sections (1.2.2, 1.5.1, 1.6.2 and 2.3.4), inheritance has many pitfalls because it provides white-box reuse. With WeaveJ, an implementation can only access the public interface of its parent implementations; that is, at compile time parents only expose their public interface to their children (black-box inheritance). This restriction allows WeaveJ to exchange implementation classes based on a binding file (see next section). The client programmer can even exchange an implementation provided by the framework.
The kind of inheritance used by WeaveJ for composition is referred to as implicit inheritance. The kind of inheritance described in this section is different: it allows an implementation of a particular interface to inherit from an existing implementation of the same interfaces. This is explicit inheritance between concrete classes. Therefore, all the harmful effects of white-box inheritance are available. Explicit inheritance between implementations should only be used sparingly in the design of a framework. It is more or less meant as a last resort feature. For example, it can be used by programmers who need to fix a broken framework component. They create a new component which explicitly inherits the framework component in order to override the broken functionality.
WeaveJ composes components through inheritance. The composite inherits from all the components it is composed of. Consequently, WeaveJ allows composites to override public methods implemented by their components. Programmers should therefore use this option sparingly. If a system’s composites frequently override their component’s methods, something is wrong with the system’s design.
One of the issues not covered yet is how WeaveJ selects an implementation
given a particular interface. WeaveJ uses a configuration file which
consists of a list of pairs, each binding an implementation to an
interface.19
The syntax of the bindings file is XML. An example of a simple bindings file is
shown below.
<bindings>
<import package="de.tub.test"/>
<bind interface="X" class="XImpl">
<bind interface="de.tub.test.Child" class="ChildImpl2"/>
</bind>
</bindings>
The example demonstrates all features of WeaveJ’s binding mechanism:
The scope of the inner binding is its outer binding. The inner binding will only be used for the composition of the implementation given in the outer binding. Outside the outer binding the default binding of the inner interface is be used. In the above example the interface X is bound to the implementation XImpl. Suppose that XImpl is a composite that requires a Child implementation from the de.tub.test package. Also suppose that the bindings file of package de.tub.test binds Child to ChildImpl. This binding is temporarily overridden by the inner binding, which binds Child to ChildImpl2 from the current package. This has the effect that for XImpl’s composition ChildImpl2 will be used instead of ChildImpl. Compositions of other implementations will use the default ChildImpl again.
Nested bindings in combination with WeaveJ’s support of inheriting implementations provide a powerful tool for client programmers. They are able to fix things that are broken in the framework or toolkit they use. They can add debugging facilities to their own components or the framework. And the debugging facilities can be switched on and off only by modifying the bindings file and running the WeaveJ. No source modifications are necessary.
In using WeaveJ for framework design, a big improvement over traditional object-oriented libraries can be achieved: even without access to the sources, functionality can be inserted and modified at any location in the framework. Traditional OO-libraries allow functionality to be added to the leaves of the class-hierarchy only.
WeaveJ’s binding mechanism enables programmers to postpones the decision about which implementation is used for a particular interface. The framework author can make suggestions in form of default bindings but the client programmer makes the final decision. Furthermore, programmers can “fine tune” the mapping between interfaces and implementations by using nested bindings.
In section 2.1.1 I already mentioned that object-oriented software gains flexibility and reusability by avoiding to mention names of concrete classes for object creation and variable declarations. In an WeaveJ-based framework interfaces are used to declare member variables and method signatures. Also, names of the implementations are unknown at compilation time. However, object creation requires the concrete class of the new object. Currently, there are three design patterns addressing this particular problem:
The Abstract Factory, Factory Method and, to some extent, Prototype patterns all
The Abstract Factory is just a specialized form of the Factory Method pattern. This means that there are essentially two distinct alternatives to built-in object creation: (1) the prototypical approach which uses duplication of objects and (2) the constructional approach which uses a virtual constructor. The prototypical approach works especially well with object composition because it is often easier to clone an existing object structure than to assemble a new one. Examples of object composition were given in sections 1.6.2 and 2.1.
Since WeaveJ is a static technique and not based on object composition, it uses a more constructional approach for object creation: for each bound interface WeaveJ generates a surrogate class. The name of the surrogate class equals the name of the interface plus Inst. This surrogate class can be used to create objects using the operator new. The surrogate classes are created during WeaveJ’s GenStub phase. Another phase called Resolve replaces all references to a surrogate class with a reference to the implementation class bound to the surrogate’s interface.
Of course, object creation needs to be parameterizable; that is, constructors should be allowed to have arguments. For this purpose, interfaces may define a special initializer method. The initializers name equals the interface’s name except that the first letter must be lower case. WeaveJ uses the initializer methods’ signature for the constructor of the surrogate. It also adds a constructor with that signature to each of the interface’s implementations. The surrogate’s constructor is empty because the surrogate will never appear in the final program. The implementation’s constructor forwards the call to the initializer method.
Figure 2.22 shows an example with three interfaces (Foo, Bar and FooBar). It illustrates the configuration after WeaveJ was run in GenStub mode but before Compose mode. Foo has two implementations and Bar has one. Because FooBar extends Foo and Bar, FooBarImpl is be composed of one Foo and one Bar implementation. For every interface there is a surrogate (FooInst, BarInst and FooBarInst) and a stub (FooStub, BarStub and FooBarStub). Stubs will be discussed in section 2.6.8.
In order to be instantiated, a surrogate must not be abstract; that is, it must contain a body for all methods required by its interface. Therefore, each surrogate is a complete implementation of its interface with empty methods. The constructor of the surrogate FooBarInst has the same signature as the initializer fooBar(). Clients use the new FooBarInst(x,y,z) constructor to create an instance of a FooBar implementation. WeaveJ’s Resolve phase will replace this with new FooBarImpl(x,y,z), provided that FooBarImpl is bound to FooBar. Why doesn’t the example list a constructor for FooBarImpl? Because there simply is none after the GenStub phase. WeaveJ’s Compose phase generates a constructor later. This constructor contains code to forward the call to FooBarImpl’s fooBar(arg1,arg2,arg3) method.
Although this looks complicated, it is so only with respect to WeaveJ’s internals. The WeaveJ user is only confronted with simple rules. To be more precise, the user should
Two more issues are worth noting. First, the initializers may be overloaded just like constructors in standard Java. The second point is about what in standard Java is known as constructor chaining. Java requires that the first thing in a constructor is a call to the parent’s constructor. If there is none Java will insert a call to the parent’s default constructor. Furthermore Java also prohibits access to this until the parent’s constructor has been called.
In WeaveJ-based designs the job of standard Java constructors is done by
initializer methods. Therefore, the initializer of a composite implementation
should at least forward the call to each of its component’s initializers. This is why
fooBar() has three arguments. The first argument is passed to foo(), the second
and third are passed to bar():
class FooBarImpl extends FooBarStub implements FooBar {
void fooBar( Arg arg, Arg1 arg1, Arg2 arg2) {
foo( arg );
bar( arg1, arg2 );
...
}
...
}
The above list of conventions must be extended accordingly: WeaveJ users should
also include code in their composite’s initializer, which then forwards to the
components’ initializers, if there are any. Because users are likely to overlook the
above conventions occasionally, WeaveJ offers the optional Check phase. When
WeaveJ is run in Check mode it verifies whether (1) all initializers in a
implementation are declared in the interface and (2) each initializer forwards to
the components’ initializers.
The following list summarizes the advantages of WeaveJ’s object creation mechanism:
|
|
The framework creation is done by the framework provider. The framework distribution contains all framework packages including the interface-classes, a bindings file per package and the stub and implementation classes (this section treats stubs and surrogates as one). Figure 2.23 shows that framework provider and client programmer essentially perform the same steps. The different parts of the framework distribution join the client creation process at different stages. The client creation process ends with two stages not found in the framework creation process: composition and resolution. Note that the resolution eliminates the stubs and bindings file. Neither appears in the final program distribution.
The following list summarizes all stages (FP = framework provider, CP = client programmer):
FP and CP are just roles. Of course, these roles can actually be performed by a team rather than individuals. The frameworks also needs to be tested, which is best done with test client programs. Consequently, the framework provider also performs the client programmer role.
Furthermore, real development will most likely consist of many iterations of the stages presented here. These iterations are not shown in figure 2.23. If developers used a make utility in order to automate the development process, every stage of the process would map to a target in the makefile.
Although I do not want cover many implementation details of WeaveJ, some of the issues might be relevant in this context. I assume that the reader has a basic understanding of Java’s underlying class-file structure and byte-code instructions [LY99].
As mentioned before, WeaveJ is a post-compilation tool which analyzes and modifies the byte-code of compiled Java classes. Although the format of Java class-files is well documented, reading, modifying and writing it is a complex task. This is because a binary Java class is a highly referential data-structure. Fortunately, several byte-code engineering libraries are freely available. The libraries I considered were Markus Dahm’s BCEL library, CFParse and JikesBT, the latter two being provided by IBM.
JikesBT was chosen because it provides a fairly complete object-model as an abstraction of the class-file structure. This object-model is similar to the one provided by Java’s built-in reflection capabilities with the difference that reflection is read-only. The other two libraries were not appropriate because they either operated on a low level revealing all the class-file details (BCEL) or were too limited in their object-model (CFParse).
JikesBT’s object model completely hides the constant-pool of the class file. JikesBT replaces all references to items in the constant pool with references to objects in the object-model. The invokevirtual opcode, for example, expects the constant-pool index of the called method’s signature. The object-model represents both the opcode and the called method, i.e. the target, as objects referencing each other.
At some point during the development of WeaveJ I found that direct modification of the constant pool would be convenient too. Suppose that one particular method is invoked in many different places in a class-file and that the target of all these invocations (calling sites) needs to be changed to a different method. Without access to the constant-pool, an iteration over all calling sites is required. With access to the constant-pool one just needs to patch the constant-pool entry holding the target’s name and signature. This works because all calling sites of a particular method refer to the same constant-pool entry.
During composition WeaveJ uses JikesBT to modify or set the parent-class of other classes. JikesBT provides a method which does that but it only changes the symbolic reference to the parent-class. There are other places throughout a class in which the parent-class is referenced. When a Java class overrides one of its ancestors’ methods, the super keyword can be used to call the overridden method from within the overriding one. Every time ’super’ appears in the Java source, the compiler generates an invokespecial instruction. This instruction does not only refer to the called method but also to the class in which this method is defined. For example, during compilation of code like super.someMethod() the inheritance chain is searched upwardly for the first parent-class that contains someMethod(). The generated invokespecial instruction refers to this class. This has the effect that the average Java class will be sprinkled with symbolic references to its ancestors.
This issue also applies to WeaveJ, since WeaveJ supports inheritance between implementations and allows composites to override components’ methods. When WeaveJ sets the parent class of an implementation, it changes each invokespecial to refer to one of the new ancestors. To find the ancestor, WeaveJ mimics what Java does when compiling the super keyword.
WeaveJ’s GenStub phase creates a stub and a surrogate for each bound interface. Surrogate classes were described in section 2.6.6. Besides serving as the base for the surrogates, stubs also may be used as the base of implementations. In WeaveJ-based systems, a composite implementation is allowed to override methods defined in its components. An overriding method usually invokes the overridden one. In Java this is done using the super keyword. Evidently, if there was no stub the compiler would refuse to compile code like super.someMethod(). The stub class therefore contains dummies for all methods required by each component interface. Figure 2.24 illustrates this. It shows a composite interface XY, its stub XYStub and one implementation XYImpl. XYImpl overrides foo() defined in XImpl. Before composition, the invokespecial instruction in XYImpl.foo() references XYStub.foo(). After composition, this invokespecial refers to XImpl.foo().
The example also shows that stubs are only needed during development. The fully composed program will not contain any stubs or surrogates. Atomic components do not have to inherit a stub because the stub would be empty anyway. The current version of WeaveJ still generates a stub even if it is not needed.
It is also worth noticing that the stub does not declare to implement any interface. Although, XYStub has everything needed to satisfy the interfaces X and Y it does not implement these interfaces. This is in order to oblige the programmer to explicitly specify which interface an implementation class implements. Remember that when extending class, i.e. inheriting it, the inheriting class will also take over all interfaces the inherited class implements.
During composition and stub generation WeaveJ generates additional class files. WeaveJ takes special care not to overwrite existing classes and to ensure unique names for the generated classes.
The names of the stubs and surrogates are determined by postfixing the interface name with Stub or Inst respectively. Command line options control whether WeaveJ’s GenStub mode places class files in a special shadow directory or in the directory of the current package. The directory structure of the shadow directory parallels the package directory structure. Moreover, the shadow directory must be listed in the classpath environment variable for the other stages of the development process to find the generated classes.
Section 2.6.3 made clear why classes need to be duplicated during the composition stage. How WeaveJ names and places the duplicates is best explained using an example. For this purpose I want to recycle figure 2.24 which shows the classes XYImpl, XImpl and YImpl composed through inheritance. It is very important to keep in mind that every class might also be part of other compositions in which it inherits a different class generating a different version of the class. Every such class must be named uniquely. WeaveJ does so by postfixing the class name with the name of the class it inherits. For the above example this means that YImpl is actually named YImpl+XImpl and stored in YImpl+XImpl.class. Accordingly, XYImpl is named XYImpl+YImpl+XImpl.
Although the separator “+” violates Java’s rules for class identifiers it can still be used because this restriction is only enforced by the compiler whereas WeaveJ operates on the byte-code level. Using an illegal character for separation has the advantage of not interfering with non-generated classes.
If XImpl belonged to a different package than YImpl and XImpl, de.tub.test for example, the name of YImpl would actually be
The next chapter demonstrates how WeaveJ can be used to implement a truly reusable framework for graphical editors. Although, the current version of WeaveJ is sufficient to prove the feasibility of such a framework, WeaveJ is still a prototype which lacks many important features. I would like to discuss the missing features briefly.
Transparent composition could be used for a variety of purposes like debugging support on behalf of the framework. The framework author would be able to write debug implementations of some or all of the framework’s interfaces. The debug implementation would write a message to stdout and then forward the call to the real implementation. The client programmer would then have the option of inserting a debug implementation before the real implementation in the serialized composition graph.
Currently, something similar can only be done using inheritance between implementations (section 2.6.4). This has the disadvantage that the programmer needs to specify the concrete parent class of the debug implementation. With transparent composition the debug implementation of a particular interface can be used for every implementation of that interface.
Furthermore, WeaveJ naming scheme for generated duplicates of class files produces long class names (see section 2.6.8). The generated names may exceed Java’s or the platform’s file name limits.
The version 0.2 of WeaveJ underwent a few changes which I would like to document here.
Foo foo = new FooInst()
|
is now written as
Foo foo = new Foo$()
|
This chapter describes the design and implementation of JDraw, a prototypical framework for GUI applications written in Java. It is prototypical in that it is far from being finished and in that it can be used as a site for further experiments. But more importantly than that it proves the feasibility of the concepts introduced in this thesis. JDraw shows how the WeaveJ tool (presented in chapter 2) can be used to develop application frameworks which are more reusable than frameworks whose design focuses on single class inheritance. It also features a flexible, intuitive and predictable layout algorithm which is based on a simple and mechanical model.
At this point I would like to give a summary of the previous chapters. Chapter 1 contains an analysis of current GUI toolkits and application frameworks. It shows how class inheritance limits the framework author as well as the application programmer who uses the framework. It also illustrates how Design Patterns introduce another level of reuse: the reuse of concepts and designs. The chapter concludes that pattern weaving, i.e. the ability of incorporating more design patterns into the framework as it evolves is crucial for achieving reusability.
The criticism of inheritance is not new. There are already alternative approaches, some of which are subject of chapter and 2. The latter also contains an evaluation of traditional techniques to weave Design Patterns and it shows their inadequacy for larger systems.
When I started my work on JDraw I realized that a dedicated post-compilation tool was needed to achieve a scalable and elegant way of pattern weaving in the Java programming language. Consequently, I wrote the WeaveJ tool, which is described in detail at the end of chapter 2. Having WeaveJ at hand, I felt equipped well enough to write a GUI application framework.
The layout of visual languages such as UML diagrams or Petri-Nets is of special interest in my group. Hence the layout algorithm is probably the most advanced subsystem of JDraw.1 The layout subsystem was inspired by UniDraw [VL90] and InterViews [LCI+92] (see chapter 1). It extends UniDraw’s Connector-Glue model and merges it with InterViews’s Box model which was in turn inspired by Donald Knuth’s TeX.
The problem with proving reusability is that it takes time. Almost every application framework claims to be reusable. But this claim remains unverified until several other people have actually tried to use the framework for their applications and more importantly extended it. Since JDraw and WeaveJ are not even close to being finished it would not be a good idea to use them in real-world applications. On the other hand, adding new subsystems and incorporating new Design Patterns into JDraw in the future should be easy.
The JDraw framework can be seen as a collection of subsystems. Using pattern weaving reduces the dependencies between subsystems because the functionality of the subsystems can be kept in separate classes. Java’s AWT and Swing for example, both being single rooted class hierarchies, merge their subsystems’ code in their base class Component or JCComponent. In JDK 1.3 the source for Component contains more than 5000 lines of code including documentation and the compiled class file is 42k. Component incorporates code for the following subsystems:
The main goal for the development of JDraw was not only to avoid overweight base classes (also see 2.3.4) like Component, but to avoid the idea of base classes at all. In JDraw each subsystem comprises one or more key-interfaces, each describing one particular aspect of component functionality. The key-interfaces provide a facade2 for the other classes in that subsystem. Sometimes the key-interfaces correspond to roles in design patterns. For each key-interface there is at least one implementation class.
The most notable difference to traditional frameworks is that there is no single component implementation in JDraw. Instead there are implementations of aspects of component functionality. It is the framework user, i.e. the application programmer, who decides which aspects of component functionality the application’s components should comprise. The WeaveJ tool is then used to merge the aspect implementations, i.e. the classes implementing key-interfaces.3
This has the following consequences:
One might ask, whether it is really necessary to use a proprietary tool like WeaveJ to achieve an alternative object-oriented architecture. The answer depends on the implementation language and the size of the system. C++, which has much more language features than Java,4 has alternatives to single inheritance built in: parameterized and multiple inheritance. Both are examined in chapter 2.
In small-scale systems overweight base-classes can be avoided by splitting them up
into multiple classes. But this technique does not really work for larger systems
like GUI toolkits or application frameworks. To illustrate that I want to recycle
the above example of AWT’s Component. The developers of AWT could have split
Component into a chain of several inheriting classes, each implementing one of the
aspects mentioned earlier. The disadvantage of this method is that the
aspects cannot be merged freely because the inheritance relationships are
predetermined. Supposed that the base classes in this hypothetical AWT design
were LayoutComponent  VisibleComponent
VisibleComponent  EventComponent
EventComponent  ChildComponent (arrows denote inheritance) it would be impossible, for example,
to have a child component that is not a visible component. This is okay for
small systems in which the number of aspect combinations is limited and
predictable. Another serious disadvantage of single inheritance designs is
that no one other than the framework authors can add new aspects (see
section 1.2.2).
ChildComponent (arrows denote inheritance) it would be impossible, for example,
to have a child component that is not a visible component. This is okay for
small systems in which the number of aspect combinations is limited and
predictable. Another serious disadvantage of single inheritance designs is
that no one other than the framework authors can add new aspects (see
section 1.2.2).
As mentioned before, JDraw’s architecture is split into subsystems. Each subsystem focuses on one particular aspect of component functionality. Figure 3.1 shows the subsystems necessary to get roughly the same features as in current frameworks like JFC (Swing).
The layout subsystem calculates the geometry (size and position) of components based on the assumption that they have rectangular bounds. It consists of the more lower level abstraction of Rulers and Links (a in-depth description of each subsystem follows in later sections). Rulers are connected to each other through links. Thus rulers form a network in which their relative position to each other is constrained by links. On top of that level rests the Box abstraction. Box is one of the key-interfaces of the layout subsystem. Box does not completely hide the lower level but makes managing rulers and links much easier. Because of that it can still be seen as an instance of the Facade design pattern.
The appearance subsystem takes care of how components draw themselves. It defines the two key-interfaces Glyph and Surface. Glyphs can render themselves on a Surface. Obviously, any rendering presumes knowledge about geometry. This is why the appearance and the layout subsystems have to collaborate intensively. This collaboration manifests in the merger-interface GlyphBox which merges the Glyph and Box functionality. Any visual component which wants to be laid out by the layout subsystem and render itself using the appearance subsystem should incorporate GlyphBox functionality.
__________________________________________________________________________
GlyphBox provides a good opportunity to summarize WeaveJ’s working principle.
Remember that for every interface there is at least one implementation class.
Consequently, there is a Box and a Glyph implementation, namely Glyph_ and Box_ .
The merger interface GlyphBox extends Glyph and Box (note that for interfaces Java
does allow multiple inheritance). It also adds some more functionality. The
implementation of the GlyphBox interface is done by the class GlyphBox_ . It is
important to understand that GlyphBox_ does not have to re-implement Glyph or Box
functionality. Instead WeaveJ automatically composes all three classes through
inheritance such that GlyphBox_ has Glyph’s and Box’s functionality at its
disposition. This can be done in two different ways: a) GlyphBox_ extends Glyph_
which extends Box_ or b) GlyphBox_ extends Box_ which extends Glyph_ .
__________________________________________________________________________
The consistency, history, properties and interaction subsystems, which are outlined in the following paragraphs, are not yet implemented.
Section 1.1.3 on page 5 explains why a framework should incorporate some means of retaining the consistency between an application’s internal data structures and their external representation. This is the domain of the consistency subsystem which is based on the Observer design pattern. One of the first appearances of this pattern can be found in UniDraw [VL90] which is described in section 1.3.1 on page 17. In JDraw, the registration and notification of views is taken care of by the Subject implementation Subject_. Any application class, whose instances make up an applications internal data should incorporate the Subject functionality. For every application specific subject there should also be at least one application specific view. The view uses one any of the built-in components (see below) or application specific components to define its behaviour and appearance.
The history subsystem manages snapshots of object state according to the Memento pattern. This provides applications with some kind of Undo mechanism which is considered a standard feature of todays applications.
The interaction subsystem is responsible for mouse and keyboard interaction. The related patterns are Command and Chain-Of-Responsibility. How this is supposed to work is best explained using an example. When the user clicks a mouse button, the interaction subsystem notifies all listeners. Suppose the listener is some kind of Box. It can then use the Box.bounds() method to test whether the cursor position is within its own bounds. If the cursor position is within the listeners bounds it will handle the mouse click in whatever way it likes. If the cursor position is outside the listeners bounds it will forward them to the next listener.
The properties subsystem manages the components properties. The idea of putting this component aspect into a separate subsystem is borrowed from the InterViews toolkits decouples the properties from the components. For a motivation of this refer to section 1.4.2.
A GUI application framework isn’t worth much if it does not offer actual components like text-labels, buttons, text-fields and the like. Currently JDraw has text-labels, beveled-borders, simple-borders and filled rectangles.
The term component is used in this context synonymously for user-interface-control.
I prefer the term component because a) AWT and Swing use this term and b) it
emphasizes the fact that components are composed of other component. There are
two different kinds of composition in JDraw: class composition and object
composition. The class composition is done by the WeaveJ tool as explained
earlier. Object composition is best explained using an example. This is the source
for the Button interface:
public interface Button extends Box {
void Button( Surface surface, String label );
void text( String text );
String text();
}
We can see that a Button is a Box and that can be created by passing
a surface and a label for the button. This is the source for the Button
implementation:
public class Button_ extends Button$$ implements Button {
private Label label;
public void Button( Surface surface, String label ) {
Box();
this.label = new Label$( surface, label );
enclose(
new Border3D$( surface,
new Border$( surface, 3, this.label )
)
);
}
// ... more methods ...
}
Have a look at the initializer method Button. The first action it does is to forward
to the Box initializer. It then creates a new text-label object and stores a reference
to it. After this it creates a border object to which it passes the label object. This
is because a border should decorate the label. Finally it calls the enclose()
method in Box which ensures that the button’s bounds are identical to the
border’s bounds (figure 3.2.
The result is a button object which decorates a border object which decorates a label object. This is object composition. But there is also class composition: The Button interface extends the Box interface. This causes WeaveJ to compose the implementation class Button_ with the implementation class Box_ such that the former directly or indirectly inherits the latter.
One more point is worth noticing. The Button interface extends the Box interface.
But a box has no means of rendering itself onto the screen. How can
the button be visible if it can’t be drawn? The answer is that it doesn’t
need to. All rendering is done by the border and label component. These
are GlyphBox extensions as can be verified by looking at their interface
sources:
package de.tub.jdraw;
public interface Border3D extends GlyphBox {
void Border3D( Surface surface, Box box );
}
package de.tub.jdraw;
public interface Label extends GlyphBox {
public void Label( Surface surface, String text );
public void text( String text );
public String text();
}
In GUI applications there are many different ways of laying out components. The most rudimentary way is to have the application programmer hard-code a components’ absolute coordinates. Obviously, this is a tedious and non-intuitive task. There are two common solutions to this problem. One is interactive component layout in which the programming environment (IDE) sports some kind of form-designer. The application programmer uses the form designer to place and size components interactively. However, absolute layouts, even if they are generated interactively, do not adjust well to varying display hardware.
The other approach is to have the application compute the layout. This is done based on constraints which can be either implicit to components or specified explicitly by the programmer. Examples for such constraints are: “This component is below that component” or “This component must be at least 42 pixels wide” or “This component should be twice as wide as that component” or even “This component must not overlap that component”. The set of constraints and the set of components form a system which has to be solved rather quickly to allow the user to adjust the layout interactively, e.g. to resize forms or to drag the splitter bar in split windows. Therefore, the framework designer has to find a trade-off between the universalness of the constraints and the time it takes to solve them.
JDraw’s layout subsystem has the following attributes: it is flexible, predictable and intuitive to use.
Flexibility: JDraw’s layout abstraction is general enough to cover all of the above ways of component layout. It can be used to specify intra-component constraints (constraints implicit to components) as well as inter-component constraints.
Predictability: With increasing complexity of constraint systems the layout mechanisms of some traditional GUI toolkits show unexpected behaviour. This is mainly due to an incorrectness of the layout algorithm. Often the algorithm is only applicable to special cases of constraint configurations. JDraw’s layout subsystem is based on a very simple but general model which makes it easy to predict its behaviour.
Intuitiveness: GridBagLayout, AWT’s and Swings’s most powerful layout model uses seven parameters in each dimension to constrain the layout.5 Specifying these parameters in an application often turns into a trial-and-error process. The existence of several different layout models amplifies this problem. JDraw has a single type of constraint which covers everything: the link. Links are analogous to mechanical springs that can be expanded and compressed up to a certain length. I claim that a mechanical model like this makes specifying layout constraints much more intuitive. However, whether something is intuitive or not depends on individual experience. For a description on how JDraw’s layout subsystem can be used to emulate GridBagLayout see the text-frame on page 285.
JDraw’s layout subsystem takes care of computing the geometry of components. It is not directly responsible for rendering components although a change in a component’s geometry will most likely trigger a re-rendering in the appearance subsystem. The collaboration between these two subsystems is subject of section 3.4.
The layout subsystem is divided into two layers. The lower level layer is built around the abstraction of rulers and links. The higher level Box abstraction utilizes rulers and links to define the location and size of boxes (figure 3.3).
A ruler stands for a value in 1-dimensional discrete space. Whether this value is a x- or a y-coordinate is irrelevant at least at this level. The interpretation of the ruler’s value is left to higher layers. The Box layer, for example, knows which ruler needs to be interpreted as a x-coordinate (vertical ruler) and which one needs to interpreted as a y-coordinate (horizontal ruler). A box uses vertical rulers for its left and right edges and horizontal ones for the top and bottom edges.
A link represents a connection between two rulers constraining their relative distance to each other. The distance of two rulers connected through a link is identical to the length of the link. Links and rulers form a network. The process of solving the network results in a discrete value for the length of each link and thus the relative position of each rulers. The rulers’ absolute positions in the network can be determined afterwards based on the link-lengths and the assignment of the value 0 to a single arbitrary ruler--the anchor.
For now, links can be seen as mechanical springs spanned between rulers. This physical analogy is one of foundations for the intuitiveness of JDraw’s layout model. A mechanical spring has a well-defined dependency between its length s and the mechanical force F. This dependency, also known as the characteristic s-F-curve is an inherent attribute of each link. For ideal springs this curve is a linear function whose slope is defined by the strength of the spring. The point in which this curve intersects the s-axis (F = 0) defines the natural length of the spring. The curve is descending to correctly represent the direction of the force. If the spring is expanded beyond its natural length, the force will be directed opposite to the s-axis. Hence, the force is negative for any length greater than the natural length. If the spring is expanded to lengths shorter than its natural length, the resulting force will be directed as the s-axis.
Consider two mechanical springs whose ends are tied together as shown in figure 3.4e. They form a parallel combination in which both springs will influence each other’s lengths. The combination of both behaves like one single equivalent spring whose strength is the sum of the original springs’ strengths. I will give a more precise description of the equivalent spring’s properties shortly.
|
|
Within JDraw the term link is used instead of spring because links feature a more generalized representation of the s-F-curve which covers more than what can be described using the spring analogy. Also, the term link stresses on the fact that they are connections between rulers.
The s-F-curve of unlimited links extends indefinitely in both directions of the s-axis. Their curve is defined for all s-values. Links can optionally be limited; that is, their length can only vary within certain limits. The curve of limited links is only defined for s-values within the limits. A spring which has a minimum (maximum) length and which can be expanded (compressed) indefinitely is called a min-link (max-link). JDraw represents infinity with a dedicated value which is very large compared to common display dimensions.
The terms compression and expansion may be misleading in this context. JDraw uses a signed value to represent lengths. Therefore, s-values can also be negative. A link whose length is smaller than the link’s natural length is considered compressed even if the current length is negative and its absolute value is greater than the absolute value of the link’s natural length. In other words, a link is considered compressed (expanded) if it causes a positive (negative) force.
The force of a constant-link does not depend on its length. The corresponding s-F-curve is a horizontal line; that is, its slope is zero. A force-less link is a constant link which carries no force at all and is represented by the curve F = 0. A fixed link does not have any degree of freedom at all. Its length and force are fixed. The corresponding s-F-curve degenerates to a single point. The mechanical analogy to a fixed spring is a strut. Figure 3.5 shows some common s-F-curves.
I have shown that parallel combinations of two links can be reduced to a single equivalent link but I have not yet given a formal definition of how the equivalent s-F-curve can be determined given the curves of the two parallel links. The equivalent curve of to parallel links can be computed by adding the forces (F-values) of both original curves point-wise. This can be verified intuitively by picturing two identical springs--it needs twice the effort to expand both springs in parallel as it needs to expand just one.
Likewise, the equivalent curve of a series combination of two links as shown in figure 3.6 can be computed by adding the lengths (s-values) of the two original curves point-wise.
Intuitively, it is obvious that the length of the equivalent spring in a series combination is the sum of the lengths of the original springs. It may not be obvious at first that their forces do not add. Imagine a physical experiment in which a weight is hanging on one end of a spring whose other end is fixed. The weight’s gravitational force elongates the spring according to the spring’s strength. Now imagine that the weight is attached to a series of two springs of the same kind. Each spring’s length will be identical to their length in the single-spring configuration. This shows that both springs are subject to the same force.6
Series and parallel combinations of more than two links can be reduced iteratively by reducing the first two links to one link and then combining the result link with the third one and so on.
Figure 3.7 shows examples of series and parallel combinations. Diagram d and e in this figure are of special interest. Diagram d shows a series of two links in parallel with a parallel combination of two links; that is, diagram d shows the parallel combination of the links in diagrams b and c. The link in diagram b has much narrower limits than the one in diagram c. The parallel combination of both has the same limits as the link in b. One observes that the equivalent curve of any parallel combination is only defined for s-values at which all of the participating links are defined; that is, the range of the equivalent curve is the intersection of the ranges of the participating links.
Diagram e shows a series combination (the one of diagram c) in series with a parallel combination (the one of diagram b). What makes the curve in this diagram special is that it consists of multiple segments. This can also be explained intuitively: Remember that the series combination of two springs (as in c) is weaker than each original spring (a) and of course much weaker than their parallel combination (b). If one expands the series combination of b and c, c will expand more than b because c is much weaker than b. Therefore, c will reach its limits earlier than b. After c reaches its limits, b is the only spring that can be stretched further. Spring b is stronger than c and so it will require more effort to do so. This is why the last segment of the curve is steeper than the middle segment. The same applies to compression.
|
|
So far I have shown what links and rulers are and how series and parallel combinations of links can be reduced to single equivalent links. This section is about the solution of the entire network. The goal in solving the network is to determine the length of all links. The solution algorithm can be divided into two phases. During the first phase the network is reduced in order to simplify the problem. Only when the network is reduced to a certain configuration (dangling link, see below) it is possible to determine the length of the remaining link. This is because all the links that influence each other’s lengths are combined in a single equivalent link. The second phase determines the length of each link as the network is reconstructed to its original form.
The reduction phase of the algorithm consists of the following steps.
Figure 3.8 shows the reduction of a simple example network. It also introduces a graph notation more suitable to this level of consideration. In this notation rulers become the nodes of a undirected cyclic graph and links become the arcs7 between the nodes.
Using the graph notation it is easy to identify series combinations of links as well as dangling links. A dangling ruler is defined using the graph notation as a node with just one arc. This arc represents the dangling link. A node with exactly two arcs represents the middle ruler in a series combination of two links. A dangling ruler and its link can be reduced by simply removing them from the network. A series combination is reduced by removing the middle ruler in conjunction with its two links and connecting the equivalent link between the two outer rulers. Figure 3.9a and b depict the reduction of dangling links and series combinations of links.
|
|
In order to optimize the reduction process, parallel links are not stored as distinct arcs. Instead, parallel links are combined to one equivalent link as soon as the network is constructed; that is, the links are bundled. During the solution of the network this equivalent link is used. The equivalent link has to be updated only when one of the links in the bundle is changed or when links are added to or removed from the bundle. The bundling of links is possible because the reduction of parallel combinations of links is structurally neutral since it does not involve the elimination of rulers.
A parallel combination can still occur as a result of the reduction of a series combination. When eliminating a series combination, the algorithm has to check whether there is already a link connecting the two outer rulers of the combination as shown in figure 3.9c.
At times there are multiple possibilities to reduce a particular network structure. For example, the series combination in figure 3.10 can also be regarded as two dangling links. Some reductions are more expensive than others and the algorithm tries to pick the less expensive one.
Whenever a dangling link is eliminated the algorithm determines this link’s operating point. The operating point of a dangling link is defined as the s-F-point in the link’s s-F-curve which has the least absolute force (see figure 3.11).
|
|
Note that a dangling link may be the result of the reduction of a whole sub-network. A sub-network is defined as the maximum set of connected nodes which is connected to the remainder of the network through exactly one arc. For example, the network in figure 3.12 consists of two sub-networks. All links in a sub-network are related; that is, they affect each other’s length. The length of links belonging to different sub-networks is not related. After all related links are reduced to a single equivalent dangling link it is possible to compute the sub-network’s operating point. The operating point of the original links can later be induced from their sub-network’s operating point. After the last remaining dangling link is eliminated, the network consists of a single ruler and the reduction phase is finished.
The algorithm’s second phase reconstructs the network. Eliminated rulers and links will be put back into their original position. When a series or parallel combination of links is reconstructed, the algorithm will use the operating point of its equivalent link to compute the operating points of the original links. The length of a link is defined as the s-value of its operating point.
The operating point of links in a parallel combination will be determined by searching the s-F-curves of the original links for the s-value of the equivalent link’s operating point. Likewise, the operating point of links in a series combination can determined by searching for the F-value of the equivalent link’s operating point. Figures 3.13 and 3.14 illustrate what can also be verified using the spring analogy. Springs in a series combination are all subject to the same force whereas parallel springs have the same length. The process of computing the operating point of links is also referred to as link-settling.
|
|
|
|
The reduction of the network is a destructive operation. It removes rulers and links from the network or replaces links with new ones. This brings up the question of how the network is reconstructed. So far the algorithm was described as being divided into two iterative phases. The real algorithm is recursive. Whenever the network is modified, the affected links and rulers are stored in local (automatic) variables and recursion starts all over. Upon return from each level of recursion, the original state of the network is reconstructed using the state saved in these variables. This mechanism effectively uses the call-stack to save the necessary undo information. Nevertheless, the algorithm can still be described as being two-phased. The reduction happens during the descending phase of the recursion while the reconstruction and link-settling is done during the ascending return phase.
Eventually, the network is reconstructed to its original state and the operating point, i.e. the length of every link is known. In order to determine the absolute position of each ruler, i.e. its distance to the anchor ruler, an additional traversal of the network is needed.
The algorithm terminates with three possible results:
Combinatorial un-solvability occurs when parallel links with incompatible limits are detected. Remember that the range of the s-F-curve of a parallel combination’s equivalent link is the intersection of the original links’ ranges. If the intersection is empty, i.e. if the ranges of the original links do not overlap, the parallel combination is undefined.
The chance of structural un-solvability results from the limited set of combinations that the algorithm can reduce. Speaking in graph-theoretical terms, the algorithm is able to eliminate nodes with a degree8 of 1 (dangling rulers) and 2 (series combinations) but not more. The simplest structurally unsolvable network is the complete graph of the third degree, i.e. the smallest possible graph that only has nodes of degree 3 (see figure 3.15).
|
|
In order to analyze structural unsolvability further, a short excursion into the field of electrical circuits is necessary. So far I have only mentioned the mechanical analogy to layout networks in which links are represented by mechanical springs. On the other hand, the terms “series” and “parallel combination”, “characteristic curve” and “operating point” indicate that there is another physical analogy.
Links can also be regarded as resistors in an electrical circuit in which the rulers represent the wiring between them. Resistors have a linear characteristic U-I-curve just as springs have a linear s-F-curve. Even the laws for calculating the total resistance of a series or parallel combination of resistors are similar. One important difference between these analogies is that a series combination of springs may result in a multi-segmented equivalent curve whereas the U-I-curve of a series of resistors is always a single line.
For resistors there is a law which describes how to convert triangle- to star-combinations of resistors and vice versa. This may indicate that there is a similar law for springs. The above mentioned difference between the series combination of resistors and that of springs suggests that this law cannot be translated directly. If such a law existed, it could be used to eliminate the middle ruler in figure 3.15b.
__________________________________________________________________________
The UniDraw [VL90] framework treats the glue (the equivalent of JDraw’s links)
as resistors in an electrical circuit. The advantage of this approach is that
the laws for the conversion of series, parallel, star and triangle combinations
can be directly translated into the layout algorithm. UniDraw’s layout solver
is more versatile than JDraw’s because it is able to process more complex
structures.
The problem with this approach is that the electrical analogy is less intuitive than the
mechanical one. Imagine a limited force-less link in series with a limited forceful one.
When this series combination is expanded, one would intuitively expect that at first
the force-less link stretches while the forceful one remains relaxed. Only after
the force-less link reaches its limit, the forceful one would begin to stretch as
the expansion continues. JDraw implements this kind of behaviour correctly.
__________________________________________________________________________
Fortunately, such unsolvable structures do not occur very often in real applications which is why I think that JDraw’s approach presents a good trade-off between intuitiveness and versatility.
The previous sections have described the layout solution process from a more general and algorithmic point of view. It is also interesting to have a closer look at the implementation of the algorithm. Rather than describing the implementation at the level of methods and classes, I want to explain the data-structures, optimization techniques and some numeric effects related to the algorithm.
Any algorithm that performs a recursive traversal of a cyclic graph has to detect these cycles in order to prevent infinite recursion. The usual method to do so is to use a boolean flag for every node. This approach only works if it is guaranteed that all the nodes are visited during the traversal. Only in this case the next run of the algorithm can assume all marks to be in a uniform state. Traversing the graph beforehand in order to reset all flags turns out to be tricky because this traversal has to detect cycles too.
JDraw’s layout solution algorithm cannot guarantee that the traversal visits every node. It cancels the traversal as soon as it finds a reduce-able combination. Hence, JDraw uses a integer number instead of a boolean flag. The version number is incremented before the traversal and every node with a different version number is considered unvisited. This way it does not matter whether the node was visited during the last traversal.
At this point, the overall description of the layout solution process is complete. The following sections cover some implementation issues without getting into the details.
Lazy reduction is an optimization technique employed by the reduction algorithm. I would like to give a brief motivation for this optimization technique.
Unlike mechanical springs, links are directed; that is, they have a designated start and end. Using directed links and signed values for the length s and the force F avoids ambiguities in the solution process. If links were undirected, there would always be two possible solutions for any series combination as shown in figure 3.16. In order to correctly denote a link’s orientation, the graph notation has to be extended such that arcs are depicted as arrows.
The reduction of series and parallel combinations defined earlier in this section is only applicable when the combined links co-directed, i.e. when they have the same orientation. In case they are not co-directed, one of them has to be inverted. The inversion of a link mirrors its s-F-curve by the negating every point’s s- and F-value.
It is easy to construct cases in which a single oppositely directed link in a network of otherwise co-directed links can cause repeated inversion during the network’s reduction (figure 3.17a).
|
|
Networks like the one in figure 3.17a are common in real-world layouts. It is therefore strongly recommended to avoid the inversion of links if possible. Initially, the reduction is lazy; that is, only combinations of co-directed links are reduced. The example in figure 3.17b shows that lazy reduction skips the elimination of the left-most ruler because its links are not co-directed. The lazy reduction does not involve any inversions at all. Evidently, skipping anti-directed links takes less time than repeatedly inverting them. In case no reduce-able combinations can be found lazily, the algorithm becomes eager and remains so until the network is solved or its un-solvability is detected.
The Box layer, which will be examined in the next section assists the application programmer in creating networks in which most links are co-directed. In these networks lazy reduction prevents the inversion of links completely.
One of the design decisions I made during the development of JDraw is not to use any of Java’s built-in container classes for the basic layout data structures but to implement the data structures manually. This has the following reasons:
Two of the layout data structures are of particular interest and will be examined below:
The s-F-curve of links is represented as a singly linked list of s-F-points. A s-F-point is a tuple (s,F). The points in the list represent only samples of the s-F-curve. The curve’s segments between the samples is assumed to be linear. Thus, any s-F-point between the samples can be interpolated linearly using the two neighbouring samples. This representation implies that the samples are sorted by their s-value. This s-order is one of the central invariants.
The following operations need to be performed on s-F-curves:
The first two operations produce a new list. Assuming s-order, the F-sum can easily be computed by iterating over the two lists simultaneously, i.e. managing two current sample points at the same time. The current sample with the smaller s-value is chosen and the other curve’s point at the chosen s is interpolated. The F-values of the sample and the interpolated point can then be added yielding the result point. Finally, the variable holding the chosen sample is advanced to the next sample.
When computing the s-sum, another invariant needs to be established: the F-order. If the samples in the list are sorted by their F-values, the s-sum can be computed in very much the same way as the F-sum.
Both invariants in conjunction restrict the set of links that can be processed by the layout algorithm to either
Monotonously increasing links are active links whose effect is interesting but hard to grasp intuitively. Consequently, JDraw uses the set of monotonously decreasing links. The key observation is that this restriction makes all operations on curves O(n), where n is the number of samples in the curve.
One reduction step is O(m) where m is the number of nodes in the graph, i.e. rulers in the network. This is because in the worst case the entire network needs to be scanned for a reduce-able combination. Since every reduction step reduces one node, the reduction is finished after m steps. This makes the entire algorithm O(m2 * n) under the assumption that the number of links is in the order of the number of rulers, i.e. that the graph is sparse. This assumption will be justified in section 3.3.4.
There are two standard ways to implement a graph: adjacency lists and adjacency matrices. For sparse graphs--and the layout network is sparse--using the adjacency matrix representation is not recommended because many of the matrix cells will be unused. Therefore, JDraw uses a data structure similar to adjacency lists.
The problem with standard adjacency list implementations is that the arcs in an undirected graph usually have to be represented using two symmetric adjacency list entries. Figure 3.18 shows an undirected graph fragment and its symmetric adjacency list representation. The redundancy of two entries wastes
|
|
The first option to reduce this overhead is to simply drop one of the references as shown in figure 3.18c. This solution saves space but needs two iterations to find out whether two nodes in an undirected graph are connected.
The solution implemented in JDraw merges the two list entries into one, halving the number of necessary objects. There is one adjacency entry per arc which is why I will refer to these entries simply as arcs.
An entry in the standard adjacency implementation has two attributes: a reference to the graph node and a reference to the next entry. The arcs in the alternative solution have four attributes. This can be made plausible by thinking of arcs as having two ends: a major and a minor end. The arc holds node and successor references for each of its ends. This leads to the four attributes majorNode, minorNode, majorNext and minorNext.
Rather than accessing these attributes directly, they are read and written through
accessor methods. For standard adjacency lists these methods would look like
this:
Node to() { ... } // gets the node reference
void to( Node to ) { ... } // sets the node reference
Arc next() { ... } // gets the successor reference
void next( Arc arc ) { ... } // sets the successor reference
In the alternative solution all these methods have an additional parameter which
is why I refer to this solution as parameterized adjacency list.
Node to( Node from ) { // gets the node reference
if( from == majorNode ) {
return minorNode;
} else {
return majorNode;
}
}
// sets the node reference
void to( Node from, Node to ) { ... }
// gets the successor reference
Arc next( Node from ) { ... }
// sets the successor reference
void next( Node from, Arc arc ) { ... }
Links can be limited or unlimited. The s-F-curve of unlimited links extends into infinity. Infinite values can cause problems when they occur in arithmetic operations. Therefore, unlimited links are represented as limited ones with very large limits--large compared to standard display dimensions in pixels. The other option is to represent infinity as a dedicated value and make all necessary arithmetic operations handle infinity specifically.
The advantage of simply using large values for infinity is that arithmetic operations do not have to treat infinite values in a special way, provided that there is enough headroom. The headroom is a range of numbers reserved for the results of inflationary operations. An arithmetic operation applied to infinite arguments may yield an even greater result as long as the result is within the headroom. The current value for infinity is ±(215 - 1) = ±32.767. The necessary amount of headroom depends on the operations being used. Multiplication needs much more headroom than addition. Fortunately, addition is the only inflationary arithmetic operation used in the layout algorithm. Given the above definition of infinity, using signed 32-bit integers provides 31 - 15 = 16 bit of headroom.
The available headroom constrains the maximum length of chains of series
combinations of unlimited links. This is because the s-F-curve of unlimited links
ranges from s = - to s = +
to s = + and the reduction of a series combination adds
their s-values. The equivalent link of a series combination of two unlimited links
ranges from s = -2 *
and the reduction of a series combination adds
their s-values. The equivalent link of a series combination of two unlimited links
ranges from s = -2 * to s = +2 *
to s = +2 * . A headroom of 16 bits allows for chains of
216 unlimited links. This seems to be a lot but the headroom has to be reduced for
reasons explained shortly.
. A headroom of 16 bits allows for chains of
216 unlimited links. This seems to be a lot but the headroom has to be reduced for
reasons explained shortly.
Arithmetic calculations with s- and F-values occur frequently throughout the solution of the network. Some of these calculations involve a division. For example, determining the operating point of a dangling link means finding the point in which the link’s s-F-curve intersects the s-axis. If this point lies between two samples, it can be determined using the following interpolation:
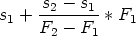
.
Obviously, dividing integer numbers can lead to non-integer (fractional) numbers. The following techniques can be used to deal with this in a computer program:
The IEEE floating-point standard distributes the discrete floating-point values non-uniformly across the total range. With single-precision (8-bit exponent, 23-bit mantissa) floating-point numbers, there are 223 discrete values in the interval [1, 2) = [20, 21) but as many values in [223, 224). This means that the resolution is 1 in the interval [223, 224) and 2 in the next interval [224, 225) in which only every second integer value is represented. Starting with this interval, the resolution of floating-point numbers is worse than that of 32-bit integer numbers.
A resolution worse than one (> 1) introduces an error into the layout computation. Experiments have shown that this error increases throughout the reduction of the network and that it influences the quality of the solution. Because of that, the headroom has to have a resolution of 1 and the range of numbers greater than 224 (for single-precision numbers) cannot be used for the headroom. Using ±(215 - 1) to represent infinity gives 23bit- 15bit = 8bit of single-resolution headroom.
Fixed-point numbers use a fixed number of bits for the fraction. The advantage of the fixed-point representation is that one can use fast integer operations and integer variables to store the numbers. The layout algorithm uses 32-bit fixed-point arithmetic with 8 bits of fraction. This effectively reduces the headroom to 16 - 8 = 8 bit which is the same as with 32-bit floating-point numbers. This means that fixed- and floating-point numbers are equivalent as far as the amount of headroom is concerned. On the other hand, fixed-point arithmetic is as fast as integer arithmetic and thus faster than floating-point arithmetic.
It needs to be stated that the fixed-point format is used internally only. The upper layers of the layout subsystem deal with non-factional numbers; that is all external layout coordinates are discrete pixel values. For example, the external pixel coordinate 1 is represented as 1<<8, where << is the binary shift operation and 8 is the number of fraction bits.
The last issue I want to describe briefly is related to constant links. Constant links and force-less links in particular are used in the Box layer to constrain the size of boxes without adding a force to the network. Text labels, for example, should never be smaller than the width and height of the text they contain. This can be enforced by using a force-less min-link (see figure 3.5 on page 210) constraining the width and height of the label.
Constant links introduce ambiguities into the layout algorithms. In a series combination of two constant links their length (operating point’s s) can be chosen arbitrarily as long as the sum of their lengths is equal to the length of the combination’s equivalent link. An example of this is shown in figure 3.20. The operating point of a series combination’s equivalent link in figure 3.20c is at (20, 0). The figure shows two of the many possibilities to choose the operating points of the original links: 8 + 12 = 20 and 5 + 15 = 20.
|
|
The ambiguity can be resolved by prioritizing the links using an asymmetry found
in series combinations of co-directed links: one of the links is incoming whereas
the other one is outgoing. Consider the the series combination in figure 3.21c.
Link  is incoming and link
is incoming and link  is outgoing. When determining the operating points
of two constant co-directed links in a series combination, the algorithm
prioritizes the incoming link. The prioritized link will be assigned the
minimum possible length (s
is outgoing. When determining the operating points
of two constant co-directed links in a series combination, the algorithm
prioritizes the incoming link. The prioritized link will be assigned the
minimum possible length (s ) and the outgoing link will fill the remainder
(s
) and the outgoing link will fill the remainder
(s = s
= s +
+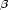 - s
- s where s
where s +
+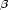 is the s-value of the equivalent link’s operating
point.
is the s-value of the equivalent link’s operating
point.
|
|
The layout algorithm avoids the reduction of anti-directed links to the effect that--at least for well-formed networks--the prioritizing scheme can rely on reductions of co-directed links. The worst thing that can happen during the solution of an ill-formed network is that it takes longer time to solve it and that the ambiguities are not resolved as expected. Furthermore, the Box-layer assists the application programmer in the creation of well-formed networks.
Furthermore, it is important to create well-formed networks, i.e. networks in which links are co-directed. Otherwise the ambiguities are not resolved consistently and the solution needs more time and resources due to the repeated inversion of links. The application programmer should not be held responsible for creating well-formed networks, since that is an internal optimization within the layout subsystem.
Consequently another architectural layer is needed in order to relief the application programmer. This layer is called the box-layer because it is built around the Box interface. The Box interface represents the layout aspect of a component. This implies that components have rectangular bounds. The advantage of the box-layer is that laying out boxes can be done without having to deal with rulers at all. The box-layer also reduces the number of occasions in which links have to be dealt with.
An simple example shows how easy it is to compose boxes (see also figure 3.22):
new Label$( "Sacramento" )
.stack( new Label$( "Eureca" ) )
.stack( new Label$( "San Louis Obispo" ) )
.pack( new Label$( "Bakersfield" ) )
.stack( new Label$( "Los Angeles" ) )
A box is defined by its four edges: top, left, bottom, right. Each of the edges is defined by a ruler. The width (and height) of a box can be optionally constrained by connecting links between its left and right (or top and bottom) rulers.
The Box interface has methods to
The pack() method composes boxes horizontally whereas stack() composes them vertically; that is a.pack(b) puts box b to the right side of box a and a.stack(b) puts box b underneath box a. Method a.pack(b) puts a null-link between a’s top ruler and b’s top ruler, between a’s bottom ruler and b’s bottom ruler and between a’s right ruler and b’s left ruler. Method stack() does something equivalent (figure 3.23a and b).
Both methods return the box that encloses the composition. For example, a.stack(b) returns a box whose top, left and right ruler are the corresponding rulers of a and whose bottom ruler is b’s bottom ruler. Note that pack()’s and stack()’s result box shares its rulers with the argument boxes. The sharing of rulers is a substantial feature of the box-layer. It will be examined shortly.
Because pack() and stack() return a value of type Box, calls to this methods can be chained as in a.pack(b).stack(c). In this example, box c will be put underneath a and b.
The method enclose() (figure 3.23c) puts one box inside another box. For example, a.enclose(b) puts b inside a.
All the above-mentioned methods are just front-ends for the real workhorse of the Box interface: the glue() method. This method “glues” two boxes by connecting any of their rulers using a given link. It can also connect two rulers of the same box (see also ”Ruler Sharing” on page 280).
To restrict the dimension of a box, one uses the methods width() and height(). For example, to ensure that a box is at least 123 pixels wide one uses a.width(new MinLink(123)).10 Again, these methods are just front-ends for the glue() method. For example, width() uses glue() to span a link between the left and right edges of a box.
A text-label uses a min-link for its width. The minimum length of this link is determined using the current font’s metrics and the current text. Whenever a new text is set, the label recalculates its minimum width and sets its width-link to that length by modifying the points in the link’s s-F-curve. Because this is a modification of the layout network, it will trigger a new solution of the entire network. Modifying the s-F-curve of a link is also referred to as non-structural modification.
Note that there can be any number of links constraining a box’s dimensions. Because all these links are connected to the same pair of rulers, they will all be parallel to each other. In addition to the implicit links which are used by the framework’s built-in components to constrain their own sizes, there can be any number of explicit links created by the application programmer. References to these links are not stored directly within the box. In order to remove or modify one of them, the reference to the link has to be kept elsewhere. Every built-in component keeps references to its own implicit links. If explicit links are going to be removed or modified, the application programmer is responsible for keeping references to these links.
For any of the compositional methods there is an inverse method which undoes the effect of that method. For stack() there is unstack(), for pack() there is unpack() and so on. The inverse methods are simply front-ends of unglue() which is the inverse of glue(). The existence of inverse methods allows for dynamic structural modifications of the layout.
JDraw supports concurrent operation. The layout network is fragile data-structure which needs to be protected such that only one thread at a time can apply structural and non-structural modifications to the layout.
Every ruler belongs to a network. Consequently, every ruler object (class Ruler) holds a reference to a network object. The network object (class Net) holds information shared by all rulers belonging to one network. All rulers which are directly or in-directly connected refer to the same network object.
Threads synchronize on this network object. This has the advantage that threads modifying different networks do not affect each others operation. A thread which is about to modify the layout network, must acquire a lock object. This is done using a ruler’s lock() method which forwards to the lock() method of the ruler’s network. Only one thread at a time can hold a lock to a particular network. To release the lock, the unlock() method of a ruler has to be used. A thread can be blocked in lock() if another thread already holds a lock to that network. When the thread holding the lock calls unlock(), the following actions are performed:
This scheme only works if every call to lock() is paired with a call to unlock(). A thread which already holds a lock can call lock() again without getting blocked; that is, lock()-unlock() pairs can be nested. In this case, only the first call to lock() and the last call to unlock() have the above mentioned effect. Thus, a sequence of modifications (in one thread) can be combined, such that the solution process is triggered only once.
The layout network of rulers and links constrains the relative position of boxes with respect to each other but not their absolute position in the output device’s coordinate space. The anchor() method of the Box interface can be used to anchor the upper left corner of a box at the absolute origin (0,0).
Whenever possible, glue() tries to avoid creating a null-link between two rulers. Instead it sets the ruler in one box to the other box’s ruler such that both boxes refer to the same ruler. The sharing direction is well-defined; that is, it is predictable which box keeps its ruler (the sharer) and which box refers to the other box’s ruler. After gluing box a’s bottom ruler with box b’s top ruler by calling a.glue(BOTTOM,b,TOP), box a’s BOTTOM ruler member refers to box b’s top ruler.11
The sharing of rulers is more complicated in practice than it may appear:
All the above issues are taken care of by JDraw. A in-depth description of the sharing algorithm is beyond the scope of this paper.
The optimization techniques introduced in 3.3.3 on page 245 and 3.3.3 on page 264 assume that the layout network is well-formed. In a well-formed network all links are co-directed. A well-formed network can be easily constructed by ensuring that every horizontal link points to the right and every vertical link points downward. Hence, links between boxes always start at bottom or right rulers and end at top or left rulers. Links between the rulers belonging to one box start at the top or left ruler and end at the bottom or right ruler of that box. The box-layer implements these rules consistently.
Sometimes it is necessary that the width or height of a box changes proportionally to the width and height of another box. This can be achieved by spanning an additional forceful link across these boxes. If the strengths of both links, i.e. the slope of their s-F-curve are equal, the size of both boxes will be equal too. If one link is twice as strong as the other one, one box will be twice as big as the other box. Likewise, this applies to more than two boxes and more complex strength ratios.
All these links have to be explicitly created and connected by the application programmer. Currently, there is not much support for this in the box-layer.
The box-layer currently includes two higher-level layout constructs: arrays and matrices. An BoxArray is like a single-dimensional variable size array. Its interface is similar to that of java.util.List. The boxes in an array are either packed or stacked; that is, the array is either horizontal or vertical. Boxes can be added and removed anywhere from the array.
A BoxMatrix is like a two-dimensional variable size array. The result looks much like a spread-sheet with the exception that every cell can contain any kind of box, including matrices and boxes.
The difference between a horizontal array of vertical arrays (or a vertical array of horizontal ones) and a matrix may seem subtle. Consider a vertical array (row-array) of horizontal column arrays: the heights of boxes in neighbouring column-arrays are not related. In a matrix, the heights (widths) of all boxes in the same row (col) are equal. Figure 3.24 illustrates this.
__________________________________________________________________________
AWT’s GridBagLayout12
(GBL) can be simulated using a BoxMatrix. The GBL parameters grid-coordinate,
grid-width and grid-height directly correspond to matrix parameters.
GBL’s padding and insets parameters can be emulated using fixed links of the desired width. To do so, the actual cell content box has to be wrapped in another inset box which in turn has to be wrapped in a padding box.
The fill and anchor parameters can be emulated using forceful links which pull the cell content box to its minimum size and by wrapping the cell content box in another box. For example, if the anchor parameter is SOUTH_EAST, the bottom and right ruler of the content box has to be glued to the bottom and right ruler of the wrapping box using null links. Force-less min-links of length 0 connect the top/left ruler of the content box to the top/left ruler of the wrapping box. In order to emulate a CENTER anchor one could simply use force-full links of equal strength which push the content box into the center of the wrapping box.
The weight parameter can be emulated using force-full links whose strength corresponds
to the GBL weight. If, for example, the weightx parameter of the first cell is 2.0 and 1.0
for all remaining cells, one could use a forceful link of double strength across the width
of the first cell and forceful links of single strength across the width of the remaining
cells.
__________________________________________________________________________
Some applications may require that components can be sized and positioned using absolute coordinates. The Mover and Sizer interfaces are Box extensions which can be used for this purpose. Both are invisible boxes enclosing the box to be positioned or sized. Mover uses two fixed links (a horizontal and a vertical one) to put itself at a fixed position in relation to another box (usually the anchor box). In order to change the position of the enclosed box, Mover modifies the two fixed links accordingly. Likewise, Sizer uses fixed links across the width and height of the box it encloses. The length of these links can be set through methods in the Sizer interface. Mover and Sizer are instances of the Decorator pattern.
I chose to put this functionality in a separate interface, because most boxes will never be positioned using absolute coordinates and I wanted to avoid the overhead of two unused links per box.
According to [HHMV93] a constraint-based system for graphical editing needs at least the following capabilities:
A link in JDraw is equivalent to a linear equation on two variables, i.e. rulers. JDraw emulates inequalities by using a very large “infinite” value for the link length s. The term “multi-way” describes the property of a constraint not to distinguish between dependent and independent variables. JDraw’s links are multi-way because JDraw doesn’t prefer one of the link’s rulers to be independent. Both rulers are completely equivalent. JDraw doesn’t decide which ruler to move in order to satisfy the constraint. In fact, rulers aren’t moved (i.e. assigned a value to) during the solution process at all. The solution process only assigns values to the length of a link, i.e. the relative distance between two rulers.
The terms low latency and high-bandwidth are subject to personal opinion. Sample applications show that JDraw’s layout solution algorithm provides “interactive” responsiveness. Its performance results from the following design decisions: JDraw uses a recursive reduction process which uses the method call stack to backup the data-structure before modifying it. Furthermore, JDraw does not use container classes in order to implement internal layout data-structures. All layout data-structures are tuned for inexpensive modification during the reduction process.
Links can be added to the network and removed from it at any time. The box layer has an inverse for every operation (glue/unglue and so on).
Currently, JDraw only detects in-solvability, but it does not really offer means to debug the cause.
JDraw’s solution process has a second mode of operation--besides determining the value for each ruler, it can also determine the equivalent link between two rulers. This equivalent link describes the range, i.e. minimum and maximum length of the link. Every interactive manipulation in JDraw is done by means of adjusting the s-F-curve of a link. The range of the equivalent link can be used to restrict the range of the interactive manipulation.
JDraw implements a physical model which uses a generalized spring (link) analogy. The force parameter of a link is used to disambiguate layouts. Therefore, an under-constrained system is caused by links with a horizontal segment in their s-F-curve (see “Constant-Link Ambiguities” on page 264). JDraw resolves these ambiguities by prioritizing links based on their direction.
The UniDraw framework initially came with a layout constraint solver similar to JDraw’s. This solver is introduced in [VL90]. All in all, JDraw’s solver is an extension of the initial UniDraw solver. The authors of UniDraw later incorporated a completely different solver engine into UniDraw, called QOCA [HHMV93]. QOCA uses a variant of the simplex algorithm which can solve systems of linear (in)equalities and optimize convex quadratic functions. JDraw can only optimize piecewise linear functions: the links’ s-F curves.
QOCA is an incremental constraint solver. As opposed to JDraw which has to recompute the complete solution every time a constraint changes, QOCA keeps the current solution around in order to determine subsequent solutions when the constraint system is perturbed. This greatly speeds up the solution process. QOCA “invests” the performance gained by its incremental algorithm in its ability to solve more powerful constraints. QOCA supports systems of linear (in)equalities on any number of variables. JDraw only supports systems of linear (in)equalities on two variables per equation and without constant factors.
QOCA’s capability to optimize convex quadratic functions can be used to minimize the distance of two two-dimensional points, e.g. to compute the start and end point of the shortest possible line between two rectangles (figure 3.25a). The distance d of two points (x1,y1) and (x2,y2) is
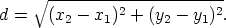 | (3.1) |
 | (3.2) |
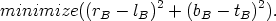 | (3.3) |
|
|
Neither QOCA nor JDraw treat points as truly two-dimensional vectors. Both handle the x- and y-coordinates of a point separately. As far as JDraw is concerned, this fact limits its physical model to springs between which the angle is 0o or 180o.
A good overview on constraints in interactive graphical applications can be found in [Bad98]. According to the taxonomy found there JDraw is a very simple form of a direct numeric solver. Direct numeric solvers, like QOCA, find a solution through symbolic manipulation of systems of equations. It might not be immediately apparent that JDraw performs symbolic manipulation. Since JDraw only supports systems of linear equations on two variables per equation the number of symbolic manipulations is limited. This obscures the fact that JDraw is a direct numeric solver.
None of the constraint systems examined in this text support disjunctions of constraints. Disjunctive constraints are very useful for interactive graphical editors but require backtracking algorithms which are currently not fast enough to provide real-time, interactive responsiveness. Research in this area seems to be focused on improving backtracking algorithms by making them incremental (see [Bad98]).
The layout sub-system takes care of the components positions and dimensions. Given this information, the components can be rendered. This aspect of components is accomplished in the appearance subsystem. The appearance sub-system determines
The appearance sub-system is built around the relationship between two interfaces: Glyph and Surface. A glyph is anything which can be rendered. A surface is something onto which glyphs can be drawn. JDraw’s appearance subsystem factors most of the control flow for the screen update into the Surface implementation. The glyphs contain only callbacks which are invoked by surface at the various stages of the rendering process. This concept was inspired by ET++ [WG95] (see also section 1.5.2) and it allows for later extension and further optimization of the rendering algorithm.
The following extract shows the interface Subject and Glyph.
public interface Surface {
void register( Glyph glyph );
void unregister( Glyph glyph );
void toFront( Glyph glyph );
void toBack( Glyph glyph );
void back( Glyph glyph );
void fore( Glyph glyph );
void conceal( Glyph glyph, Bounds bounds );
void reveal( Glyph glyph, Bounds bounds );
void beginPaint();
void endPaint();
java.awt.Graphics graphics();
}
public interface Glyph {
void render( java.awt.Graphics graphics );
void layout( Surface surface );
}
Surface.register() registers a glyph with the surface. The registered glyph will
be informed when it needs to be redrawn. The order in which glyphs register with
the surface determines their Z-order. The actual drawing process is done in two
phases: layout and rendering.
During the first phase, the surface asks all its registered glyphs to lay themselves out. For this purpose, the surface invokes layout() on each of its registered glyphs. The glyphs can then tell the surface which areas the revealed, i.e. not used by the glyph anymore, and concealed, i.e. taken up by the glyph. This done through the methods reveal() and conceal() respectively. The surface cumulates the concealed and revealed areas. The revealed areas are cleared using the background color.
All areas are represented by instances of the Bounds class, which has rudimentary operations to add and subtract bounds objects, to test for equality and whether one bounds object completely contains another one.
During the second phase, the glyphs will finally be drawn. The surface sets the clipping area to the sum of the cumulated concealed and revealed areas and invokes the render() method of each glyph that overlaps the clipping area. The clipping area will also be used to set the clip-rectangle in Java’s graphics class.
The current scheme is just a slightly optimized version of the approach of simply rendering every glyph every time the layout changes. It makes use of clipping functionality in java.awt.Graphics and tries to reduce the number of glyphs that are redrawn without need. Nevertheless, the protocol defined by the Glyph and Surface interfaces leaves room for further improvements. For example, the way how revealed and concealed areas are cumulated can be improved drastically. Figure 3.26 shows that the cumulation of two small areas yields a much bigger area. This area covers many more glyphs than actually need to be redrawn. A better algorithm keeps track of multiple revealed and concealed areas and only combines them into a bigger area if this can be done “seamlessly”.
The Z-order controls the overlapping of components. Components which are closer to the front can overlap components closer to the back. The easiest way to implement a Z-order of components is by defining a consistent order in which the components are drawn. Thus, components can be drawn on top of other components. The visual result will always be the same as long as the components are drawn in the same order.
The appearance subsystem renders components in the order of their registration. It keeps a list of glyphs and redraws the glyphs according to their order in this list. The methods toFront(), toBack(), fore() and back() can be used to control the Z-order any time after the registration.
There is no sole glyph implementation class in JDraw. Instead, there is the merger interface GlyphBox and its implementation GlyphBox_. It merges the glyph and box functionality; or more precisely, it uses the layout information provided by Box to implement the glyph-surface protocol. In most other frameworks the layout and the appearance aspect are not separated. JDraw allows for later addition of other layout mechanisms without having to throw away any of the appearance code.
__________________________________________________________________________
It is also possible to write components which compute their layout on their own.
Tool-tip windows, which can be found in almost any graphical user interface, are a good
example for this. Tool-tip windows are small boxes containing a short text which gives
context-dependent information about the component over which the mouse cursor is
currently located. They appear when the mouse is held still for a few seconds. Because
their position only depends on the location of the mouse pointer and their lifetime is
relatively short it would not make sense to integrate them into the layout of the
persistent components.
__________________________________________________________________________
Figure 3.27 shows an abbreviated class diagram of JDraw.13 All visible components (Border, Border3D, Label and Rect) are descendants of GlyphBox. Interestingly, Button is not a GlyphBox descendant. This is because it is does not do any rendering itself. Instead, it is composed of simpler components which do the rendering for it: a text label, a border and a 3D-border.
__________________________________________________________________________
It is important to understand the difference between object composition and class
composition. The Button implementation class (Button_) incorporates Box functionality
through the mechanisms of WeaveJ: WeaveJ modifies the bytecode of Button_
such that it inherits the Box_ class. On the other hand, a Button_ object is
composed of three other objects. The composition is enforced by the layout
mechanisms; that is, the 3d-border encloses the border which encloses the
text-label.
__________________________________________________________________________
There are two different ways to draw something onto the screen in Java:
JDraw uses the second approach. The World class inherits java.awt.Frame and implements the Surface interface. Rather than inheriting Frame, one could also inherit Applet or Window. Inheriting Applet would have the obvious advantage that JDraw could be directly used in web-pages.
The difference between Window and Frame is that a Windows does not have any decoration at all. At the current stage of JDraw, inheriting Frame is the easiest solution and has the advantage that frames can be resized interactively. That way, the responsiveness of JDraw’s layout algorithm can be demonstrated, without having to implement the interaction subsystem.
The second Surface extension, besides World, is Viewport. Viewport is an interesting component because it demonstrates the flexibility gained by using WeaveJ for framework development. First of all, a viewport is a surface onto which glyphs can be drawn. Consequently, the Viewport interface extends the Surface interface. The viewport displays a rectangular subsection of the glyphs it contains. It displays them on another surface which can be a World or a even another viewport. Consequently, the viewport is also a glyph. It serves as a surface to the glyphs it contains and at the same time it is a glyph on another surface which contains it.
It should be possible to use the viewport in box layouts. For that purpose the viewport is a box, as well. The combination of glyph and box is represented by the GlyphBox interface. All in all, the Viewport interface extends the Surface interface and the GlyphBox interface.
A viewport translates between two layout networks: an external network and an internal network (figure 3.28). Both networks are completely independent; that is, there is no link connecting a ruler in the external network with a ruler in the internal network. A viewport has to provide means of adjusting the rectangular subsection of the internal network it displays. This rectangular subsection is called window. In traditional GUI toolkits, the window’s location is controlled by specifying the absolute internal coordinates of the window’s upper left corner. JDraw doesn’t use fixed coordinates for anything in its layout. It uses rulers and links. Using absolute coordinates for the window’s location would not fit in this scheme very well. Therefore, JDraw uses a different approach: the viewport projects its own bounds--keep in mind that a viewport is a box in the external network--onto the internal network (figure 3.28). The boxes in the internal network can then be laid out relative to this projected box. For example, the traditional approach of using fixed coordinates for window location can thus be emulated using fixed links.
As opposed to AWT or ET++, JDraw’s update handling is synchronous; that is, there is no separate thread which does the update handling concurrently. Both, the synchronous and the asynchronous approach target the problem of batch updates. In an average application, modifications to the layout or the appearance of components often occur in bundles, i.e. batches. For example, when an application initializes a form it resets all controls on that form to suitable initial values. Setting the value of a controls requires that the control is redrawn (updated). For some controls even the layout has to be recomputed. The desired behaviour is to delay layout computation and screen update until the last control is initialized. This is because the user is only interested in seeing the fully initialized form and does not actually want to watch every stage of the initialization process.
The asynchronous approach delays screen update until the system is idle. It does so by executing the update code in a separate, low priority thread. The application thread and the update thread have to be synchronized against each other. In AWT, for example, this is done using a lock object and Java’s built-in synchronization mechanism. The disadvantage of the asynchronous approach is that it doesn’t provide precise control about when the screen-update actually happens. In most cases this is not a problem. Sometimes though, an application needs to animate certain user interface components. For example, when the application needs to inform the user about the state of a lengthy operation. At every stage of the operation, the application adds an entry to a log window. In toolkits with pure asynchronous update handling, the messages would not appear until the operation is finished which is certainly not the desired behaviour.14
JDraw’s synchronous update handling bundles batch updates and provides control
about when a screen update happens. It simply uses a counter and pairs of
increment and decrement-and-test operations on this counter. The beginPaint()
and endPaint() methods in the Surface interface represent this mechanism. Code
which modifies the appearance of components must be enclosed between calls to
these two methods. beginPaint() increments the counter. endPaint()
decrements the counter and, if the counter reaches zero, triggers a screen update.
The counter value represents the nesting depth of beginPaint() and
endPaint() invocation pairs. Only the endPaint() call of the outermost
pair in a particular program control flow triggers a screen update. In the
above example, the initialization code simply needs to be put between a
call to beginPaint() and endPaint() (actually lock() and unlock(), see
below):
// application specific code:
Label nameLabel, ..., zipcodeLabel;
void initialize( Costumer costumer ) {
surface.beginPaint();
nameLabel.text( costumer.name );
...
zipcodeLabel.text( costumer.zipcode );
surface.endPaint();
}
// JDraw's label implementation
class Label_ implements Label {
void text( String text ) {
beginPaint();
this.text = text;
// invalidate area occupied by label in order
// to ensure that the label is redrawn:
surface.conceal( bounds() );
endPaint();
}
}
In the animation example, these calls can simply be omitted. This is
because the text() method in the Label implementation already contains
them.
void log( String message ) {
messageLabel.text( message ); } |
The layout subsystem determines the size and position of boxes while the appearance subsystem takes care of drawing glyphs. Many components, (more precisely, components which are extensions of the merger interface GlyphBox) are box and glyph at the same time. Consequently, screen update and layout have to be coupled. Whenever the layout changes, i.e. whenever a ruler moves, the screen needs to be updated. The layout synchronization mechanism (see “Synchronization” on page 279) ensures that only one thread at a time modifies the layout. It also bundles the subsequent layout modifications similar to the appearance subsystem bundling batch updates. The coupling between layout and screen updated is done as follows: Every network of rulers (layout network) has an owner. The owner implements the NetOwner interface. Surface implementations like World and Viewport own networks and implement this interface. The network notifies its owner when it is locked and when it is unlocked. The owner, i.e. the surface, reacts by invoking its own beginPaint() method (on lock) or endPaint() method (on unlock).
__________________________________________________________________________
Example: The application calls Label.text() on a label to set its text. The
Label.text() method calls the Box.lock() method. Box.lock() calls the Ruler
.lock() method on one of its rulers. Ruler.lock() calls Network.lock() on
the network this ruler is part of. Net.lock() increments a network-specific
counter (after ensuring that no other thread is currently holding a lock on
this network) and calls NetOwner.onLock() on its owner. Suppose that the
owner is an instance of World. This means that World.onLock() is invoked.
World.onLock() calls World.beginPaint() which increments another, World-specific
counter.
Label.text() then determines this label’s minimum size (based on the new text
and the current font) and modifies the two min-links which are connected
between the label’s left (top) and the right (bottom) ruler. Label.text()
then calls Box.unlock() which forwards to Ruler.unlock() which in turn
forwards to Net.unlock(). Net.unlock() decrements the network-specific counter
again and solves the whole network if the counter reaches zero. It then calls
NetOwner.onUnlock() which means that World.onUnlock() is invoked. This
method calls World.endPaint() which decrements the World-specific counter.
If the counter is zero, World.endPaint() calculates the updated area and
finally redraws the glyphs intersecting that area (this includes at least the label
glyph).
__________________________________________________________________________
Roughly speaking, a call to Box.lock() leads to an invocation of beginPaint(). On the other hand, a call to beginPaint() does not lead to a call of lock(). JDraw differentiates between GUI modifications which affect the layout--these must be enclosed between lock() and unlock()--and modifications which affect the appearance but not the layout--these must be enclosed between beginPaint() and endPaint(). For example, changing the background color of a text label component (Label) affects its appearance only, changing the font usually also affects its size, i.e. the layout. This is why Label_.fontChanged() calls lock() and unlock() but Label_.foregroundColorChanged calls beginPaint() and endPaint().
In summary, the coupling between JDraw’s layout and appearance subsystems
The Consistency subsystem integrates the Observer design pattern into the JDraw framework (see section 1.1.3). This design pattern frequently occurs in GUI programming because graphical user interfaces are often representations of an application’s internal data. The Observer pattern decouples the representation from the data and provides consistency between the representations and their underlying data. The Observer pattern (and JDraw’s consistency subsystem) defines two interfaces: Subject and Observer. The Subject interface defines functionality for registering and unregistering observers. The Observer interface defines callback method which the subject invokes on each registered observer after it is modified (notification).
Although this scheme seems fairly straightforward, it raises problems when it is to be implemented in an reusable way. A reusable implementation of the Observer pattern should have the following properties: it should
JDraw’s implementation of the Observer pattern has the above properties. There
is no attach() method in the Subject implementation. Instead, the attach
operation is defined in concrete Subject subtypes which can then declare this
method using a concrete subtype for the observer argument. Knowing the
concrete observer subtype makes it possible to specify a specific notification
protocol. This satisfies the second of the above criteria.
// bank account
interface Account extends Subject {
void attach( AccountObserver o );
void detach( AccountObserver o );
// set account number
void number( String s );
// get account number
String number();
// add an transaction
void add( Transaction t );
// remove transaction
void remove( Transaction t );
// get a transaction by index
Transaction transactionAt( int position );
...
}
// bank account representation
interface AccountObserver extends Observer {
void numberChanged();
void transactionAdded( int position );
void transactionRemoved( int position );
}
This approach has a slight anomaly: since there is no attach() method in the
Subject interface it seems that every concrete subject needs to re-implement the
registration functionality and that there is not really any reusable functionality in
the abstract subject to benefit from at all. In fact, there is an attach operation
in the Subject interface. It is declared as _attach(Observer o). The
name starts with an underscore to indicate that this method should only
be called by concrete subjects and not from anywhere else in the client
application. In standard Java one would use the protected modifier for the
_attach() method in order to ensure that only subclasses can invoke
it.
__________________________________________________________________________
This is one of WeaveJ’s weaknesses: since every method declared in an interface
is implicitly public, there is no way to restrict access to the methods in an
interface. Ideally, WeaveJ would provide the ability to restrict access to the
methods in an interface based on the type of the caller. In the above case of
Subject, access to attach(Observer o) should only be granted to subtypes of
Subject.
__________________________________________________________________________
The properties subsystem was inspired by InterViews’s Styles [LCI+92]. It
implements sets of component properties. For a motivation on property sets refer
to section 1.4.2 on page 31. The central interface in this subsystem is
Properties. It represents a set of (key, value) pairs. Each of the pairs
represents a property. There can be none or exactly one property per key in a
set.
interface Properties extends Subject, PropertyObserver {
// initialize an empty property set
void Properties();
// initialize a property set to inherit another one
void Properties( Properties parent );
// attach a property observer
// this can be a component or another property set
void attach( PropertyObserver observer );
// add or set a property
void set( Class key, Object value );
// get a property
Object get( Class key );
// unset (=remove) a property from the set
Object unset( Class key );
}
As opposed to InterViews, JDraw does not use strings as property keys but class objects. Using strings to identify properties is error prone because strings are hard to keep unique and easy to misspell. Class names can be checked at compile time (using the Foo.class syntax). Furthermore, class names are automatically unique--there cannot be two classes having the equal names in the same package. This prevents conflicting property keys in case an application mixes JDraw’s built-in properties, application defined properties or even properties defined in framework extensions (e.g. third party component sets). The framework, the application and the framework extensions belong to distinct packages separating the name-space of the property keys.
The Properties interface extends the Subject interface which indicates that the properties subsystem is based on the consistency subsystem. The idea behind this is simple. Instead of treating properties as an integral part of components, a property set can be regarded as external state which is represented and thus observed by components. For every property (e.g. font) there is a corresponding concrete observer interface (e.g. HasFont). For example, a component that supports the font property simply implements the fontChanged(...) method in the HasFont interface. Whenever the font property in a property set changes, the property set notifies all observing components by invoking the fontChanged(Font font) method.
Property sets can inherit from other property sets. For that purpose, property sets are also property observers. If a child property set inherits from another parent property set, it simply observes its parent. If a property in the parent changes, the parent notifies all attached observers. Among them is the child property set which in turn informs its own observers unless the child property set overrides the changed property. In case the property is overridden, the change is not notified to the child’s observers because it doesn’t apply to them. The overridden property is not affected.
The fact that property sets are subjects and observers is an example for the subject-view duality presented in the first chapter (see section 1.3.1 on page 21).
The only way to modify a component’s properties is through the property set it is
attached to. There is no need to write a property getter for every component
class. The component only needs to implement the notification method of the
property observer interface. If a components needs a property for rendering itself,
it should cache the property value internally. This is because looking up a
property in the property set might involve looking it up in the parent property set
(or even the parent’s parent and so on). Caching a property value only requires an
additional reference field in the component class. The actual property value is not
duplicated.
// without property caching
void render( Graphics g ) {
g.setFont( (Font) properties().get( HasFont.class ) );
}
void fontChanged( Font font ) {
refresh();
}
// with property caching
private Font font;
void render( Graphics g ) {
g.setFont( font );
}
void fontChanged( Font font ) {
this.font = font;
refresh();
}
Properties are weakly typed, e.g. the set() method declares the property value argument as Object. Here, JDraw trades flexibility for type-safety. The Properties interface and its implementation support any number of property types. Adding application specific properties does not require a modification to the Properties interface or its implementation. Creating properties only requires a new Has... property observer interface and a tiny implementation of that interface.
The above features are illustrated in figure 3.29 and in the following usage example.
|
|
Property sets do not know about particular types of properties. Neither do they
know about the corresponding Has... observer interfaces. The notification
protocol between property sets and observers is weakly typed. The property
observer interface is listed below.
interface PropertyObserver extends Observer {
void propertyChanged( Class key, Object value );
}
A component may implement this weakly-typed notification protocol. The body of
propertyChanged() would contain a sequence of if-statements checking for the
property key. This is functionality that should be implemented by the
framework. Consequently, JDraw adds another strongly-typed layer on top of
the weakly-typed one. This layer is made up of the Has... interfaces
mentioned earlier. They translate the weakly-typed notification protocol into a
strongly-typed one.
// strongly typed observer interface
interface HasFont extends PropertyObserver {
void fontChanged( Font font );
}
// and its implementation class
abstract class HasFont_ ... implements HasFont {
// override untyped notification method
public void propertyChanged( Class key, Object value ) {
if( key == HasFont.class && value instanceof Font ) {
fontChanged( ( Font ) value );
} else {
super.propertyChanged( key, value );
}
}
}
HasFont_ is abstract because it does not implement fontChanged(). This method
is implemented by the actual component. HasFont_ simply translates between
propertyChanged() and fontChanged(). If the changed property is not the font
property, HasFont_ forwards to super.propertyChanged().
An interesting thing happens when a component supports more than one property (as most components do). For example, the Label component supports the font, foreground and background color properties. Consequently, it implements the HasFont, HasForegroundColor and HasBackgroundColor interfaces. WeaveJ composes the Label class by including the HasFont_, HasForegroundColor_ and HasBackgroundColor_ implementations in the inheritance chain. WeaveJ also arranges the parent-class references of the super.propertyChanged() statement in all of these implementations into a chain. The chain ends with the empty propertyChanged() method of the PropertyObserver_ implementation. The chain of if-statements in the weakly-typed solution becomes a sequence of non-virtual method calls in the strongly-typed variant. Because the method calls are non-virtual, the strongly typed solution is only slightly more expensive.
The following list summarizes areas in which JDraw needs to be extended and improved.
|
|
Many of the following terms are already well-known in the world of software engineering but sometimes they are to mean a variety of things. It thus makes sense to define our connotation.
Object: A object is an encapsulation of state and behaviour. It is not necessarily an instance of a class.
Component: This term has two distinct meanings. If not explicitly stated otherwise, I use the term component to denote a object which is part of the user interface. It does not necessarily have to be visible to the user, although most components are. I refer to visible components as widget.
The second meaning was coined by distributed component technologies like CORBA and DCOM, which use the term in a more general manner to denote the distinction between objects and components in such systems. Quoting [Szy99],
software components are binary units of independent production, acquisition, and deployment.
And more importantly
components are for composition. Nomen est omen. Composition enables prefabricated ‘things’ to be reused by rearranging them in ever new composites.
Accordingly, the major characteristics of components are composition, reuse and encapsulation.
In component oriented GUI toolkits and frameworks these two definitions of the term are related: widgets are components but not necessarily vice versa.
Component- and object-oriented programming do not exclude each other. In fact, COP can be an extension of OOP in which components are objects and described by classes.
Framework aka. application framework. A framework is a way of reusing a system’s architecture. A framework defines a whole family of systems. The difference between frameworks and libraries/toolkits is that a framework dominantly outlines the system’s architecture whereas a library specializes on one particular aspect of a system’s design. Object-oriented (component-oriented) frameworks are collections of classes (components).
Interface aka. Contract aka. Protocol: An interface is a behavioural description of an object. It is an abstract type declaration mostly consisting of operation signatures. Java has a special keyword and semantics for interfaces. In general, every class has an interface, although it may not explicitly implement one. This implicit interface consists of the class’ public methods. In C++, a class’ interface is usually specified separately from its implementation in a header file.
Components can also have interfaces. CORBA and DCOM use a special language to describe the interface of components: IDL.
Implementation: The term implementation describes (1) the incarnation of a concept, a model or a standard, (2) the realization of an interface. A class which implements a particular interface has to provide a body for every method required by the interface.
Client (code/software/class): A client is software that uses a framework or a library. The client programmer, aka. framework/library user, is someone who writes this software. This term is also used frequently when describing design patterns. Client code is code that uses a pattern but does not belong to the classes that make up the pattern.
Delegation: Delegation is a technique which composes objects (components, delegatees) into a composite (delegator) such that the interface of the composite is the sum of the components’ interfaces. The composite forwards messages to its components.
Message: A message is the atomic part of the communication between objects. Depending on the programming language messages have different semantics. In the context of this text the terms message and method are used synonymously. A message is sent to an object means that a method of that object’s class is invoked. A message is implemented by an object means that the object’s class has a method body for a particular signature.
Die noch relative junge Forschung im Umfeld der Generativen Programmierung kritisiert, daß sich die traditionelle objektorientierte Softwareentwicklung primär auf die Erstellung eines einzelnen Systems fokussiert. Die Entwicklung von wiederverwendbarer Software macht eine alternative Herangehensweise erforderlich. Wenn der Enturf eines Systems aus einer Familie von Systemen nur auf dieses eine System ausgerichtet wird, dann erscheint es unwahrscheinlich, daß die resultierende Implementierung oder Teile derselben für andere Systeme aus dieser Familie benutzt werden können.
Folglich sollten Enwickler, die an der Wiederverwendbarkeit ihrer Produkte interessiert sind, den Entwurf ihrer Software auf ganze Systemfamilien ausrichten. Die vorliegende Arbeit versucht, diese Herangehensweise zu bestätigen, indem ein generisches Anwendungsframework für grafische Benutzerschnittstellen und grafische Editoren visueller Sprachen entworfen und implementiert wird.
Kapitel 1 gibt einen Überblick über ausgewählte GUI-Frameworks, untersucht deren Design und analysiert die zugrundeliegenden Konzepte. Es zeigt die Vor- und Nachteile dieser Systeme aus der Perspektive des Entwicklers, der sie benutzt, als aus der des desjenigen, der sie erstellt, wartet und weiterentwickelt.
Kapitel 2 analysiert verschiedene alternative Enwurfsmethodiken und Implementierungstechniken. Es zeigt, wie diese angewendet werden können, um die Wiederverwendbarkeit und Flexibilität von objektorientierter Software im allgemeinen und von Anwendungsframeworks im speziellen zu verbessern.
Kapitel 3 beschreibt den Entwurf und die Implementierung eines generischen, wiederverwendbaren und flexiblen Anwendungsframeworks für grafische Benutzerschnittstellen und Editoren visueller Sprachen. Eine besonders wichtige Rolle spielt dabei die Implementierung eines objektorientierten Constraint-Solvers für das Layout der Komponenten.
[ABC+95] Ole Agesen, Lars Bak, Craig Chambers, Bay-Wei Chang, Urs Hölzle, John Maloney, Randall B. Smith, David Ungar, and Mario Wolczko. The SELF 4.0 Programmer’s Reference Manual. Sun Microsystems, Inc, 1995.
[Bad98] Greg J. Badros. Constraints in interactive graphical applications. Technical report, University of Washington, Department of Computer Science and Engineering, 1998.
[Bec00] Pete Becker. Common design mistakes. C/C++ Users Journal, 18(1), January 2000.
[BN96] John J. Barton and Lee R. Nackman. What’s that template argument about? In Stanley B. Lippman, editor, C++ Gems. SIGS Books, 1996.
[Boo94] Grady Booch. Object oriented analysis and design with applications. Addison-Wesley, second edition, 1994.
[BOSW98a] Gilad Bracha, Martin Odersky, David Stoutamire, and Philip Wadler. GJ: Extending the JavaTMProgramming Language with Type Parameters. Sun Microsystems, University of South Australia, Bell Labs, Lucent Technologies, August 1998.
[BOSW98b] Gilad Bracha, Martin Odersky, David Stoutamire, and Philip Wadler. Making the future safe for the past: Adding genericity to the javaTMprogramming language. In 13th Annual ACM SIGPLAN Conference on Object-Oriented Programming Systems, Languages, and Applications. Sun Microsystems, University of South Australia, Bell Labs, Lucent Technologies, October 1998.
[CE00] Krzysztof Czarnecki and Ulrich W. Eisenecker. Generative Programming - Methods, Tools and Applications. Addison Wesley, May 2000.
[Eck00] Bruce Eckel. Thinking in Java, page 689. Prentice Hall PTR, second edition, 2000.
[GHJV95] Erich Gamma, Richard Helm, Ralph Johnson, and John Vlissides. Design Patterns: Elements of reusable object-oriented software. Addison Wesley, 1995.
[HHMV93] Richard Helm, Tiem Huynh, Kim Marriott, and John Vlissides. An object-oriented architecture for constrained-based graphical editing. Technical report, IBM T.J. Watson, Research Center, Yorktown Heights, NY 10598, 1993.
[KLG] JClass BWT. http://www.klg.com/jclass.
[Knu84] Donald E. Knuth. The TEXbook, volume A of Computers and Typesetting. Addison-Wesley, Reading, Massachusetts, second edition, 1984.
[LCI+92] Mark A. Linton, Paul R. Calder, John A. Interrante, Steven Tang, and John M. Vlissides. InterViews Reference Manual Version 3.1. Leland Stanford Junior University, December 1992.
[LY99] Tim Lindholm and Frank Yellin. The JavaTMVirtual Machine Specification. second edition, 1999. http://java.sun.com/docs/books/vmspec.
[SA98] Sinan Si Alhir. UML in a Nutshell. O’Reilly & Associates, Inc., 1998.
[SUN] The Hotspot VM. http://java.sun.com/products/hotspot.
[Szy99] Clemens Szyperski. Component Software. Addison Wesley, 1999.
[US91] David Ungar and Randall B. Smith. Self: The power of simplicity. Lisp and Symbolic Computation: An International Journal, 4(3), 1991.
[Vel96] Todd Veldhuizen. Using C++ template metaprograms. In Stanley B. Lippman, editor, C++ Gems. SIGS Books, 1996.
[VL90] John M. Vlissides and Mark A. Linton. Unidraw: A framework for building domain-specific graphical editors. ACM Transactions on Information Systems, 8(3):237-268, July 1990.
[WG95] André Weinand and Erich Gamma. ET++ - a portable, homogeneous, class library and application framework. In Ted Lewis, editor, Object Oriented Application Frameworks. Manning Publications Co., 1995.